
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
I. Ориентация тройки векторов.
Три некомпланарных вектора в пространстве 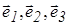 образуют упорядоченную тройку, если принято соглашение, что один из них является первым
образуют упорядоченную тройку, если принято соглашение, что один из них является первым 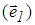 , другой - вторым (
, другой - вторым ( 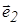 ), а оставшийся - третьим (
), а оставшийся - третьим ( 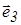 ) .
) .
Каждой упорядоченной тройке (базису) приписывается ориентация - правая и левая.
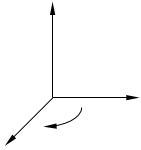
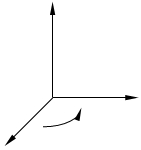
Правый базис Левый базис
Рис.1
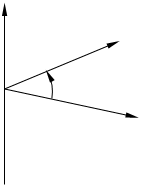
Упорядоченная тройка векторов называется правой, если из конца третьего вектора кратчайший поворот от первого вектора ко второму виден против часовой стрелки. В противном случае тройка называется левой.
Если рассматривать три ортонормированых базиса, среди которых один базис образует правую тройку, а другой - левую, то третий может быть совмещен либо с первым, либо со вторым. Тогда все ортонормированные базисы могут быть разбиты на два класса: правых и левых троек. В дальнейшем рассматриваемые базисы будем считать правыми.
II. Определение и геометрические свойства векторного произведения.
Определение: векторным произведением векторов 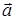 и
и 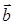 называется вектор
называется вектор 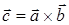 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
 |
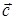
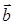 1)
1) 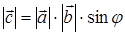
2) 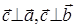
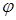 3) векторы
3) векторы  образуют правую тройку.
образуют правую тройку.
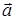
Рис.2
Если хотя бы один из векторов 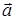 или
или 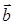 нулевой, то по определению их векторное произведение равно нулю.
нулевой, то по определению их векторное произведение равно нулю.
Пример: Пусть 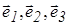 - правый ортонормированный базис.
- правый ортонормированный базис.
Тогда 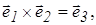
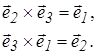
Если 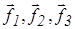 -левый ортонормированный базис то
-левый ортонормированный базис то 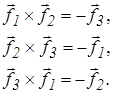
Теорема : необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
Доказательство : 1) необходимость: если 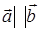 , то
, то  и
и 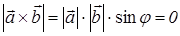 .
.
2) достаточность: если 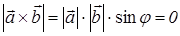 , то либо
, то либо  , либо
, либо  , тогда
, тогда 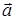 и
и 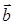 - коллинеарны по определению; либо
- коллинеарны по определению; либо 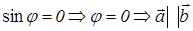 .
.
Из определения векторного произведения следует, что модуль векторного произведения равен площади параллелограмма, построенного на перемножаемых векторах.
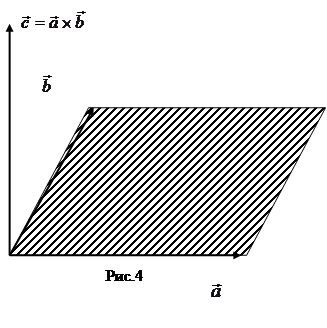
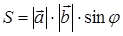 (2)
(2)
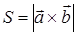
III. Алгебраические свойства векторного произведения.
Векторное произведение обладает следующими алгебраическими свойствами:
1) антикоммутативность: 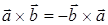 ;
;
2) ассоциативность: 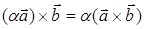 ;
;
3) дистрибутивность: 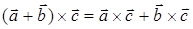 ;
;
4) для любого вектора 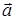 :
: 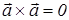 .
.
Пример : найти площадь параллелограмма, построенного на векторах
 и
и 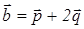 ,
,
если 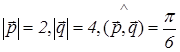 .
.
Решение: 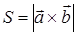 ;
;
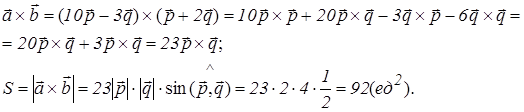
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|