Вопросы к экзамену для студентов ФТПП 1 семестр.

Вопросы к экзамену для студентов ФТПП 1 семестр.

1. Комплексные числа, действия с ними.

2. Геометрическое изображение комплексных чисел. Модуль и аргумент комплексного числа.

3. Алгебраическая и тригонометрическая форма записи комплексного числа.

4. Формулы Эйлера. Корни из комплексных чисел.

5. Пространства R и .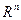

6. Понятие вектора и линейные операции над векторами.

7. Скалярное произведение и его свойства.

8. Понятие угла между векторами.

9. Условие коллинеарности и ортогональности векторов.

10. Линейная зависимость векторов.

11. Векторное произведение векторов и его свойства.

12. Смешанное произведение векторов и его свойства.

13. Виды матриц.

14. Действия над матрицами.

15. Определители второго и третьего порядков, их свойства.

16. Алгебраические дополнения и миноры.

17. Вычисление определителя разложением по строке (столбцу).

18. Понятие обратной матрицы.

19. Системы двух и трех линейных уравнений. Правило Крамера.

20. Система m линейных уравнений с n неизвестными.

21. Решение системы линейных уравнений методом Гаусса.

22. Различные виды уравнений прямой на плоскости.

23. Различные виды уравнений плоскости в пространстве.

24. Различные виды уравнений прямой в пространстве.

25. Взаимное расположение прямых, плоскостей, прямой и плоскости в пространстве.

26. Окружность и ее геометрические свойства.

27. Эллипс и его геометрические свойства

28. Гипербола и ее геометрические свойства.

29. Парабола и ее геометрические свойства.

30. Числовые последовательности.

31. Предел числовой последовательности.

32. Бесконечно большие и бесконечно малые функции.

33. Предел функции в точке.

34. Первый замечательный предел.

35. Второй замечательный предел.

36. Непрерывность функций в точке.

37. Понятие дифференцируемости функции в данной точке.

38. Связь между понятиями дифференцируемости и непрерывности.

39. Дифференциал. Приближенные вычисления с помощью дифференциала.

40. Производная функции.

41. Производные элементарных функций.

42. Производная сложной функции.

43. Производная обратной функции.

44. Дифференцирование функции, заданной параметрически.

45. Правило Лопиталя.

46. Производные и дифференциалы высших порядков.

47. Возрастание и убывание функции на интервале и в точке.

48. Необходимое условие экстремума.

49. Достаточные условия экстремума.

50. Выпуклость кривой в точке и на отрезке.

51. Асимптоты кривой.

52. Общая схема построения графика.

53. Частные производные.

54. Производная по направлению.

55. Градиент скалярного поля.

56. Дифференцируемая функция.

57. Дифференциал функции.

58. Касательная и нормаль к поверхности.

59. Экстремумы функций.

60. Наибольшее и наименьшее значения функций в области.

61. Условный экстремум.

62. Свойства сходящихся рядов.

63. Признаки сравнения.

64. Признак Даламбера.

65. Признак Коши.

66. Знакопеременные ряды.

67. Абсолютная и условная сходимость.

68. Теорема Лейбница.