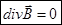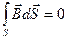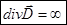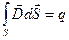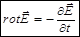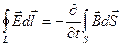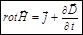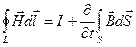Линейные токи

Уравнения Максвелла

1. Электромагнитные поля и его характеристики

Электромагнитное поле – область пространства , в которой действуют электрические и магнитные силы.

????:

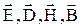
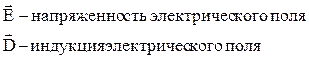
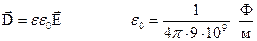
- напряженность магнитного поля

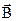- индукция магнитного поля

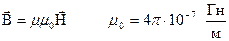
Плотность заряда

Если в пространстве имеется непрерывное распределение заряда, то плотность заряда :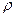

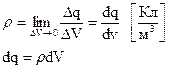
Плотность тока

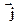- векторная величина, направление 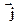совпадает с направлением тока в данной точке

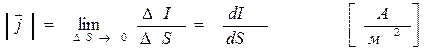
До Максвелла законы электромагнитных явлений связывали физические величины, установленные в различных точках пространства или в разные моменты времени (закон Кулона, закон Ома).

Уравнения Максвелла связывают физические величины, определяемые для одной и той же области пространства в одно и то же время.

2. Дифференциальная форма теоремы Гаусса

Закон Кулона определяет силу F, с которой взаимодействуют два точечных заряда 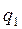и 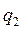, находящиеся в однородной среде

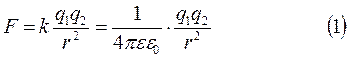
С точки зрения представлений об электромагнитном поле процесс взаимодействия между двумя зарядами выглядит так

1) точечный заряд создает в окружающем пространстве электрическое поле напряженностью

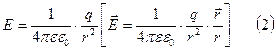
2) точечный заряд, помещаемый в это поле, испытывает действие силы

Т.е. формулы (2) и (3) содержат в себе закон Кулона.

Вероятнее (3) имеет общий характер и не зависит от причин образования поля 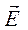. Поэтому закон Кулона содержится в (2), который удобно записать в виде:

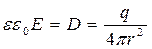
Формула зависит от среды.

На заряд поле действует с силой

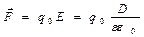
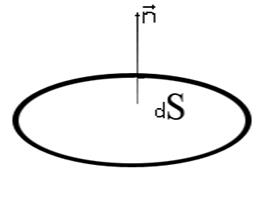
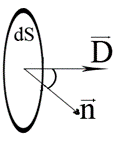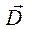Поток через площадку dS:

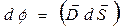
Число силовых линий ≈D

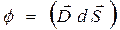- число силовых линий, пронизывающих данную площадку, если коэффициент пропускания =1.

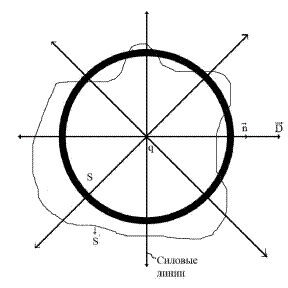
Определим поток вектора 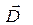через замкнутую поверхность

Внешняя нормаль 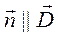, D=const

Индукция точечного заряда на расстоянии R:

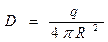
Поток через сферу радиусом R:

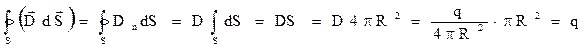
Если - замкнутая не сферическая поверхность, то число основных линий(поток) через нее будет такой же.

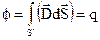
Если имеется несколько точечных зарядов, то согласно принципа суперпозиции

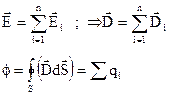
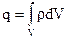
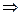
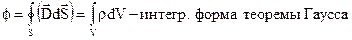
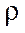- объемная плотность заряда

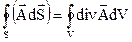- теорема Остроградского-Гаусса.

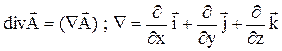
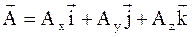
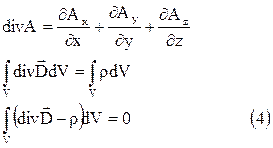
Поскольку (4) справедливо для области интегрирования V, то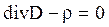

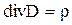- I уравнение Максвелла

Источники и стоки для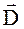

Из теоремы Остроградского-Гаусса видно, что если в объеме V 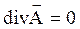, то поток вектора 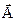через поверхность, ограничивающую этот объем =0, т.е. силовые линии A являются замкнутыми (непрерывными).

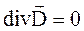- силовая линия 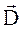или замкнуты, или уходят

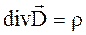- в данной точке пространства находится или источник, или сток силовых линий .

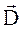Закон Ома и Джоуля- Ленца в дифференциальной форме

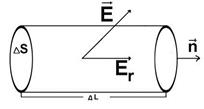Если между двумя точками существует разность потенциалов, то между этими двумя точками есть электрическое поле, которое будет перемещать заряды.

Разность потенциалов между основаниями цилиндра

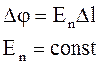
Закон Ома для этого цилиндра можно записать в виде

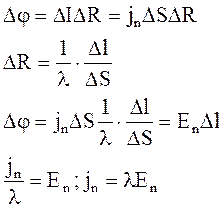
Т.к. 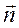выбрано произвольно, то эта формула справедлива для проекций

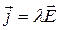- закон Ома в дифференциальной форме

Закон Джоуля-Ленца

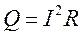( за 1с)

Применим эту формулу для выделенного цилиндра :

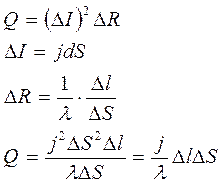
Плотность теплоты

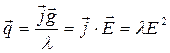
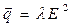- закон Джоуля-Ленца в дифференциальной форме

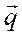- количество теплоты, выделяемое в единицу объема

Уравнения непрерывности и ток смещения.

Опытным путем установим закон сохранения заряда.

При отсутствии токов заряд, находящийся в каком-либо объеме не изменяется. Его величина 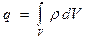. Если ток вытекает из объёма, то эта величина >0.

С другой стороны, в силу закона сохранения заряда это втекание или вытекание зарядов должно привести к соответствующему изменению величины заряда q, заключенного в объеме. За время все это изменение составит:

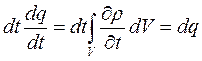
Если ток вытекает из объема, то величина 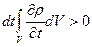, т.е.

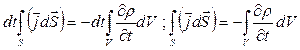
Применим теорему Остроградского-Гаусса:

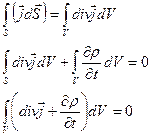
Т.к. это справедливо для V, то 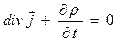- уравнение непрерывности.

Для стационарных токов заряд в каждой точке не меняется со временем

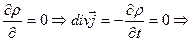нет источников или стоков, силовые линии 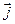замкнуты.

Если ток является переменным, то .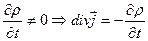

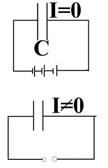Силовые линии не замкнуты, появляются источники ли стоки. Линии возникают и исчезают на зарядах.

Силовые линии замкнуть невозможно, условие невыполнимо 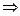ток не течет.

В случае переменного тока 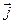прерывается на обкладках конденсатора, но I≠0

Максвелл предложил замкнуть цепь с помощью токов смещения

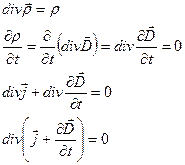
Отсюда видно, что линии векторов 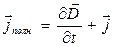всегда замкнуты.

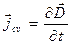- плотность тока смещения.

Вернемся к примеру с конденсатором. Когда в цепи протекает переменный ток I, заряд й на каждой обкладке изменяется, .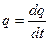

D и q связаны соотношением

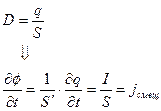
Ток смещения (перемещения электрического поля) создает вокруг себя точно такое магнитное поле, какое создавал бы ток проводимос-ти такой же плотности

Обобщение закона полного тока (уравнение циркуляции магнитного поля вдоль замкнутого контакта)

В случае постоянных токов проводимости имеет место закон полного тока: циркуляция вектора напряженности магнитного поля вдоль замкнутого контура равна алгебраической сумме токов, охватываемых этим контуром.

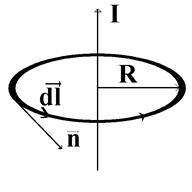Докажем для бесконечного проводника

По закону Био-Савара-Лапласа

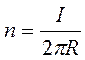
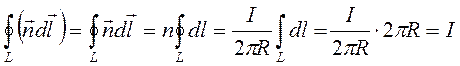
Таким образом закон постоянного тока доказан для случая прямокинетических бесконечных токов и произвольного контура в 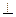току плоскости. Для того, чтобы избавиться от этого ограничения, запишем формулу в дифференциальной форме:

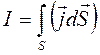
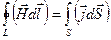
Применим теорему Стокса

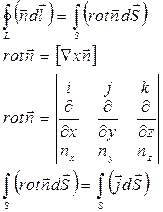
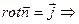ток создает магнитное поле, т.е. 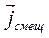создаёт такое же магнитное поле, как и равный ему ток проводимости, то .

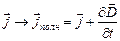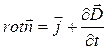- второе уравнение Максвелла

Дифференциальная форма закона электромагнитной индукции.

Закон Фарадея:

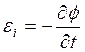
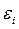равен скорости изменения магнитного потока, взятой со знаком -.

Знак – У правила Ленца : ЭДС индукции препятствует причине, её вызывающей

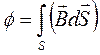
Если в цепи действует ЭДС, то

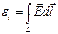
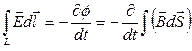
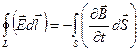
Применим теорему Стокса для :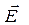

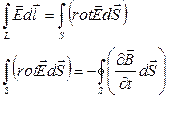
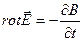- третье уравнение Максвелла

Уравнение Максвелла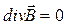

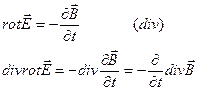
Таким образом 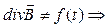При данном значении 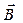величина 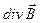такова же, какова она была при других значениях 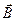, а значит и для 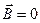. Но при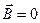 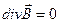, т.е. силовые линии замкнуты, магнитные заряды не существуют.

Система уравнений Максвелла

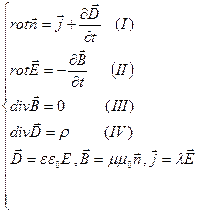
Уравнения зависят друг от друга.

Они справедливы при следующих условиях:

1) система решаема, если материальные тела, находящиеся в поле, неподвижны;

2) 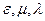не зависят от времени и от величины векторов поля;

3) В электромагнитном поле нет постоянных магнитов и ферромагнетиков.

II уравнение дает III

Убедимся, что уравнения I и IV связаны

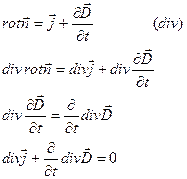
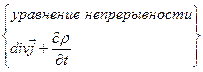
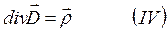
Таким образом, независимыми уравнениями являются I и II.

Выводы: 1) система уравнений Максвелла является полюс

2) система уравнений имеет единственное решение

Допустим, имеются 2 решения системы уравнений Максвелла. Тогда их разность также является решением для значений 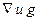, в частности для нулевых. Тогда из закона сохранения энергии следует, что разность решений 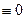, т.е. они тождественны.

Закон сохранения энергии электромагнитного поля

Чтобы иметь возможность сравнивать выводы из уравнений Максвелла с экспериментом, необходимо ещё иметь выражения энергии электромагнитного поля через векторы поля.

Рассмотрим объём V, в котором есть электромагнитное поле, токи ??????????????????(12) тепло(за счет энергии электромагнитного поля)

Закон Джоуля- Ленца в дифференциальной форме:

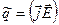- плотность теплоты

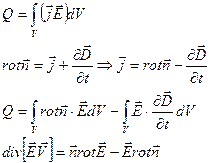
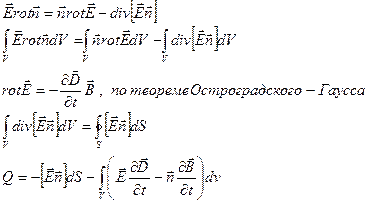
Найдем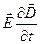

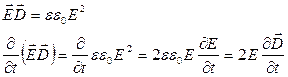
Тогда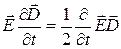

Аналогично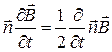

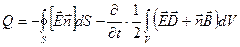
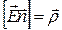- вектор Пойнтинга, характеризует излучаемую энергию

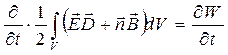- изменение энергии электрического поля.

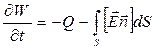- закон сохраненения энергии

Т.е. энергия электромагнитного поля изменяется в результате двух факторов: выражения теплоты и потока электронов через поверхность S, ограничивающую рассматриваемый объем.

Граничные условия

Если имеется граница раздела двух сред, то величины 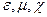меняются скачком 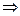скачком будут меняться и векторные величины 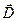и .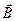

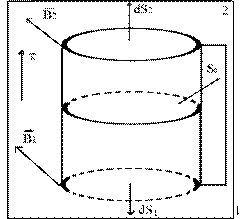Для получения числовых значений будем использовать теорему Остроградского-Гаусса и Стокса, которые применяются для непрерывных функций. Будем считать, что на границе раздела существует тонкий поверхностный слой, в котором рассматриваемые величины меняются быстро, но непрерывно. Толщину поверхностного слоя получим требуемые предельные выражения.

Граничное условие нормальной состав- ляющей .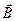

Т.к. центр 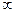малый, то 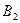и 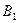=const.

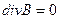
Проинтегрируем по поверхности цилиндра

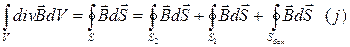
Учитывая, что взяли достаточно малый цилиндр, пренебрегаем изменением 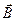, тогда можно записать

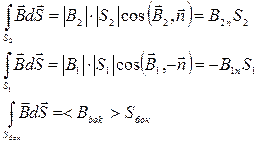
Где <Вбок> - среднее значение 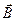на боковой поверхности.

Тогда (j) :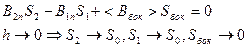

Поскольку 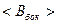- конечная, то имеем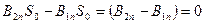

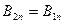Нормальная проекция 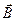не имеет разрыва на границе раздела двух сред.

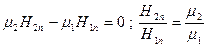
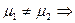нормальные составляющие 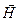на границе разрыва

Г.У. для нормальных составляющих .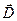

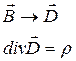
q- заряд, находящийся внутри цилиндра

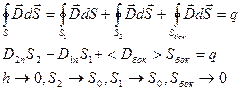
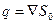- заряд на граничной поверхности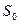

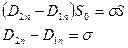
Если 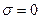(заряда нет) 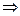разрыва нет. Если й есть, то 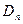претерпевают разрыв.

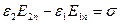
Граничные условия для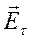

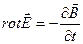
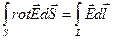- теорема Стокса

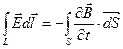, S – поверхность, натянутая на контур L.

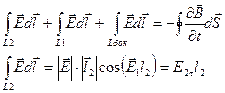
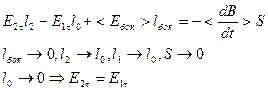
Для 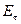на границе раздела разрыва нет

Уравнения Максвелла в интегральной форме

Записанные ране уравнения Максвелла являются дифференциальными в частных производных, т.е, это «равенства в точках».функции, с которыми нужно работать в этом случае, должны быть непрерывными и, следовательно, иметь непрерывные решения. Т.е. задача, в которой присутствует границы раздела двух сред, с помощью только систем уравнений Максвелла решена быть не может. Её необходимо дополнить граничными условиями.

Начертим таблицу

Закон эл/магнитного поля	диф. Форма	инт. Форма
Закон отсутствия магн. заряда
Закон Кулона
Закон эл/магнитной индукции
Закон Био-Савара-Лапласа

1) закон отсутствия магнитного заряда

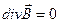
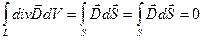- теорема Остроградского-Гаусса

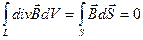, т.е. поток 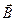через замкнутую поверхность =0.

2) закон Кулона

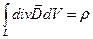
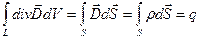
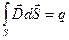
Т.е. получили теорему Гаусса: поток 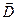через замкнутую поверхность = полному заряду, ограниченном этой поверхностью

3) закон электромагнитной индукции

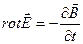
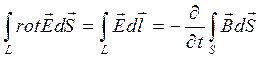- теорема Стокса

4) Закон Био-Савара-Лапласа

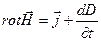
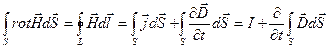
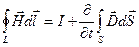
Электростатика

- величины, характеризующие поле, не меняются со временем;

- движение зарядов отсутствует, т.е. .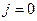

Тогда уравнения Максвелла и граничные условия имеют вид:

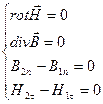
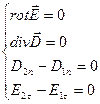
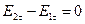- электростатическое поле

Т.е. система уравнений Максвелла разбилась на 2 независимые системы, характеризующие электростатическое и магнитостатическое поля.

Это возможно только для независимых от времени полей.

1) Электростатическое поле в однородной среде

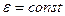
Векторное поле, rot которого =0,? Называется потенциальным 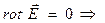поле 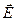потенциальное.

Для постоянного поля работа сил не зависит от пути, по которому производится перемещение, а зависит только от начальной и конечной точек.

Рассмотрим работу поля заряда по пути 132-241:

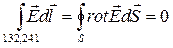, где S- поверхность, натянутая на рассматриваемый контур.

Т.о.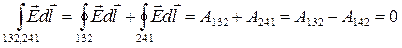

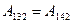
2) Скалярный потенциал

Независимость работы сил поля от пути перемещения заряда между двумя точками обуславливает существование тока скалярной функции Q, разностью значений которой в начальной и конечной точках определяется работа.

Функция Q называется скалярным потенциалом.

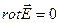
Поскольку 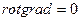, то общим решением уравнения 1 является .

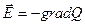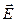«-»: направлен в сторону уменьшения потенциала.

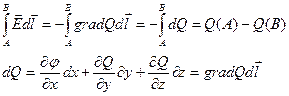
Т.е. разность потенциалов есть работа по перемещению заряда

Потенциал физического смысла не имеет

Физический смысл имеет разность потенциалов. Добавка const к значению потенциала не изменяет значения разности, т.е. потенциал определён с точностью до const. Эта постоянная произвольна, поэтому можно потенциал в любой фиксированной точке сделать равным любому наперёд заданной величине. Тогда потенциал всех остальных точек будет определён однозначно. Такая операция называется нормировкой потенциала.

В электротехнике за диаметр принимают Q земли. В теоретической физике за диаметр принимают потенциал точки, которая находится на бесконечности.

Если Е находится на бесконечности, то

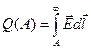(2)

3) потенциал точечного заряда

Поле точечного заряда сферически симметрично, 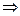потенциал тоже сферически симметричен

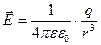
Тогда согласно 2

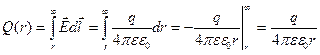
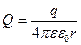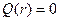, в точке, где находится заряд q/

4) Потенциал системы точечных зарядов.

Согласно принципу суперпозиции:

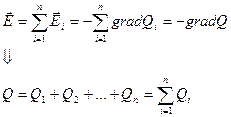
Т.е.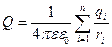

Если координаты точки, в которой находится потенциал (x,y,z), то ,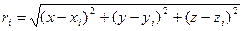

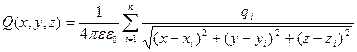
В случае непрерывного распространения зарядов с плотностью 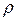можно весь объем разбить на 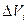, тогда

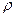qi = Vi

и в пределе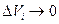

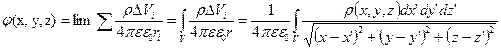
Если заряд распределен по поверхности с поверхностной плотностью 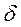то аналогично.

Потенциал в точке (0,0,0)≠ 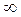. Запишем в сферических координатах:

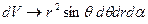
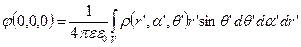
Если 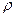-конечная величина, то и S–конечная. В общем случае формула для потенциала:

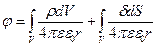
5)Уравнение для Лапласа и Пуассона

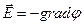
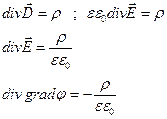
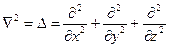- лапласиан

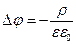- уравнение Пуассона

В области пространства, где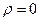

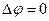- уравнение Лапласа

Д.у. удобнее интегральных, так как при их решении не требуется, чтобы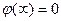

Мы доказали, что 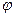в любой точке является конечным. Кроме того, должно быть конечными и производными от 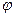в точке:

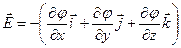
Если производное от 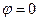, то 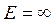что не имеет физического смысла 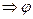- непрерывная функция.

При решении задач:

- потенциал является конечной и непрерывной функцией

- 1-я производная по координате для 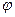является конечной

Пример: Бесконечная заряженная пластина

Имеется пластина толщиной а, заряд с объемной плотностью 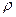. Найти

распределение 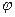в любой точке.

Предполагается, что диэлектрическая проницаемость во всем пространстве, включая пластину, постоянна и = .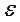

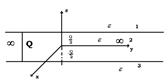Расположим плоскость хОу посередине плас-тины. При таком расположении 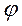зависит только от .

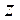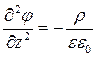
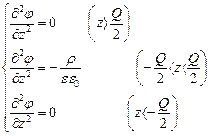
Тогда решения:

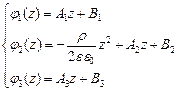
В качестве условия нормировки выберем равенство потолка средней плоскости 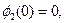, т.е. В₂=0.

Кроме того, в силу симметрии

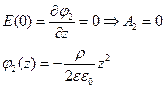
Условие непрерывности для и его производных дает уравнения:

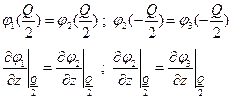
Тогда

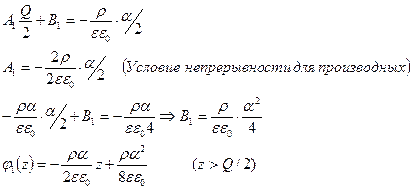
Аналогично находим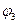

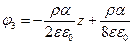
Найдем значения напряженности:

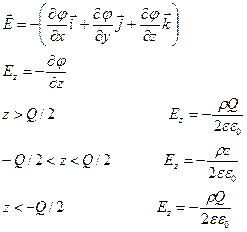
Таким образом, поле равномерно растет от средней плоскости до поверхности и направлено в противоположные стороны по разные стороны от средней плоскости. На поверхности пластины по абсолютному значению максимально и сохраняет свое значение.

Внутри проводника Е = 0.

Проводники в электростатическом поле

Проводниками называют тела, в которых при наличии электрического поля возникает движение зарядов (электрический ток).их проводи-мость 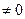. Поскольку в электростатическом поле рассматривается случай неподвижности зарядов, то

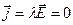
! Когда внутри имеются токи, напряженность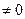

Т.к. при электростатическом равновесии поле внутри проводника отсутствует, то .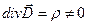

Заряды концентрируются на поверхности. Если проводник заряжается, то благодаря силам отталкивания заряды распределяются по поверхностям таким образом, чтобы поле внутри проводника = 0. Если проводник внести во внешнее поле, то заряды перераспределяются так, чтобы поле внутри проводника (сумма внешнего поля и поля, создаваемого поверхностными зарядами) = 0.

Явление перераспределения зарядов на поверхности проводника при внесении во внешнее поле называется электростатической индукцией.

Найдем поле вблизи поверхности проводников. Запишем граничные условия:

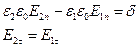
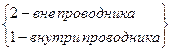
Внутри проводника поле = 0.

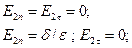
То есть

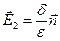- поле вне проводника направлено по нормали и равно .

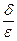Внутри проводника 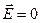(для 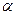любых точек проводника)

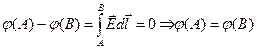
Т.е. потенциал постоянен вдоль всего проводника ;

Зависит от формы проводника, величины заряда и от распределения зарядов на других проводниках в окружающем пространстве.

Ёмкость заряженного проводника

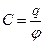
Ёмкость конденсатора

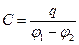
Диэлектрики в электрическом поле

Дипольны й момент

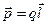
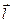-вектор, проведённый от отрицательного заряда положительному, и равный расстоянию между зарядами.

При помещении во внешнее электрическое поле диэлектрик приобретает дипольный момент(поляризуется).

Интенсивность поляризации характеризуется вектором поляризации 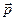- дипольный момент единицы объёма dV.

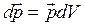
Величина вектора поляризации 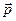в данной точке пропорциональна эл. полю в этой точке:

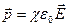
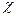- коэф. Диэлектрической проводимости.

Электрическое поле при наличии диэлектрика является суммой двух полей:

1) поля свободных зарядов, т.е. зарядов, не связанных с молекулами и атомами диэлектрика,

2) поля, возникающего за счет поляризации диэлектрика

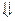
Потенциал электрического поля

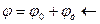потенциал, созданный поляризованными диэлектриками

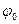- потенциал свободных зарядов;

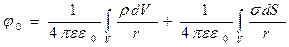
Из (1):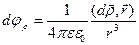

С учетом (2)

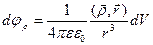
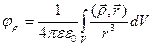
V – объем диэлектрика

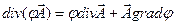
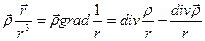
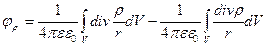
Первый интеграл можно преобразовать по теореме Остроградского- Гаусса, но для этого подынтегральная функция должна быть непрерывна.

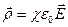
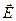на границе раздела претерпевает разрыв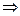 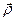тоже претерпевает разрыв.

Поэтому теорема Остроградского-Гаусса можно применить к любому объёму, если из него границу между ????? диэлектрика.

Пусть S – одна из таких границ. Выделим эту поверхность вспомогательной поверхностью 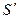. Тогда во всем оставшемся объеме

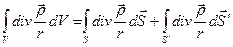
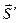- поверхность, ограничивающая рассматриваемый объём.

Пусть положительная нормаль направлена в сторону диэлектрика (2), тогда

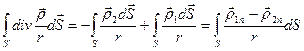
Считаем. Что все диэлектрики расположены в конечной области пространства, 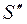- бесконечно удаленная поверхность. Тогда на этой поверхности ,

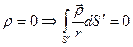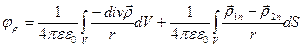
Видно, что формулы для потенциала диэлектрика и потен-циала свободных зарядов похожи.

Обозначим

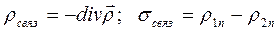
Тогда

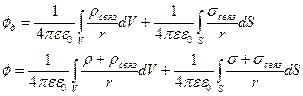
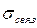возникает на границах раздела двух диэлектриков или диэлектрика с вакуумом;

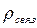возникает, когда есть неоднородность поляризации, что может являться следствием неоднородности диэлектрического или электрического поля.

Магнитостатика

- все величины не зависят от времени

- наличие постоянных токов

Система уравнений Максвелла принимает вид :

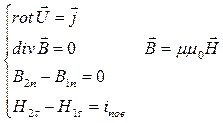
Сторонние ЭДС

Докажем невозможность постоянного тока при наличии только кулоновских сил.

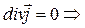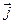Уравнение непрерывности в случае постоянных токов линии замкнуто.

Рассмотрим 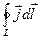вдоль некоторого замкнутого контура, совпадающего с силовой линией .

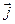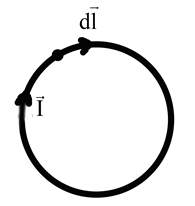Если имеется только ???? кулоновского происхождения, то , ,

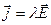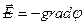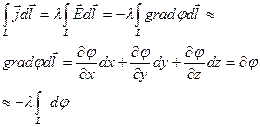
Чтобы были токи необходимы силы и поля неэлектрического происхождения. Такие силы и поля возникают в источниках тока гальванических элементах, аккумуляторах и т.д.

Эти поля называют сторонними полями, а возникающие в них силы – сторонними силами.

Поле сторонних сил характеризуется 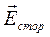, тогда

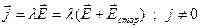
Векторный потенциал

Рассмотрим ??? поле в однородной среде

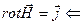магнитное поле не является потенциальным !

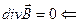* нет магнитных зарядов !

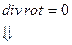
Решением * является

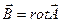
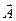- векторный потенциал магнитного поля (вектор-потенциал)

Векторный потенциал неоднозначно определяется заданным магнитным полем 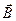. Если потенциал 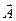описывает данное магнитное поле, то и потенциал 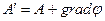описывает то же поле, т.к.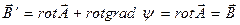

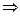на него можно наложить дополнительное условие.

В ??? это условие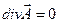

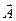является вспомогательной величиной и не имеет физического смысла

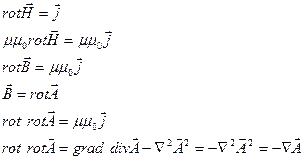
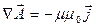- уравнение Пуассона

Это уравнение может быть записано так же в виде скалярных уравнений:

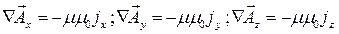
Решение уравнения для векторного потенциала можно записать аналогично решению уравнения Пуассона для скалярного потенциала:

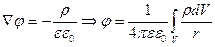
Т.е.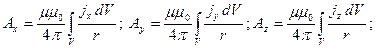

Или в векторном виде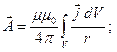

Закон Био –Савара -Лапласа

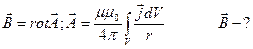
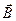определяется в определенной точке. Операция 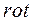- по коор-динатам точки, в которой определяется 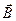не входят в .

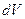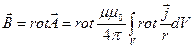
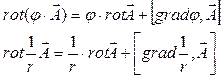
При подстановке в интеграл 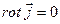(т.к. rot выполняется для точки, в которой определяется поле, а 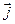зависит от координат точки интегрирования).

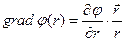, т.е.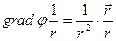

Тогда

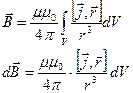-закон Био-Савара-Лапласа

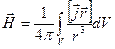
Линейные токи

В большинстве практически важных случаев постоянные токи текут по проводам, распределяясь с равномерной плотностью по сечению провода. Такие токи называют линейными.

Рассмотрим элемент dl проводника. Его объем: 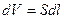, тогда

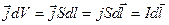
Тогда за