
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Линейная скорость сферического движения.
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Иркутский государственный технический университет
Кафедра управления качеством и механики
Реферат: на тему:
Сферическое движение твердого тела.
Выполнил студент группы АТб-12-1 Турсунов Отабек
Иркутск 2013
Сферическое движение (движение твёрдого тела вокруг неподвижной точки) — движение абсолютно твёрдого тела, при котором оно имеет одну неподвижную точку.
При движении вокруг неподвижной точки О каждая из точек твёрдого тела описывает в пространстве сферическую поверхность, центром которой является точка О.
При описании законов сферического движения принято пользоваться координатами, получившими название углов Эйлера:
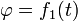 — угол собственного вращения;
— угол собственного вращения;
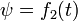 — угол прецессии;
— угол прецессии;
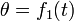 — угол нутации.
— угол нутации.
Примером сферического движения является движение прецессирующего волчка или любого тела закрученного вокруг оси, не совпадающей с осью наименьшего или наибольшего момента инерции. Другим примером является движение точек на зубьях конического катка в зубчатой конической планетарной передаче.
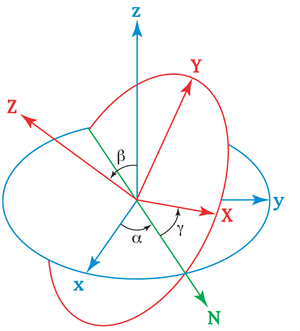
Углы Эйлера — углы, описывающие поворот абсолютно твердого тела в трёхмерном евклидовом пространстве.
В сравнении с углами Эйлера, кватернионы позволяют проще комбинировать вращения, а также избежать проблемы, связанной с невозможностью поворота вокруг оси, независимо от совершённого вращения по другим осям (см. Кватернионы и вращение пространства).
Углы Эйлера определяют три поворота системы, которые позволяют привести любое положение системы к текущему. Обозначим начальную систему координат как 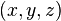 , конечную как
, конечную как 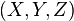 . Пересечение координатных плоскостей
. Пересечение координатных плоскостей 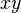 и
и 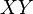 называется линией узлов
называется линией узлов 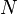 .
.
- Угол
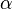 между осью
между осью 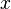 и линией узлов.
и линией узлов. - Угол
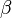 между осями
между осями 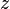 и
и 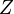 .
. - Угол
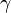 между осью
между осью 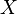 и линией узлов.
и линией узлов.
Повороты системы на эти углы называются прецессия, нутация и поворот на собственный угол (вращение). Такие повороты некоммутативны и конечное положение системы зависит от порядка, в котором совершаются повороты. В случае углов Эйлера это последовательность 3,1,3 (Z,X,Z), т.е. производится сначала поворот на угол 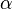 вокруг оси
вокруг оси 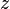 , потом поворот на угол
, потом поворот на угол 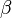 вокруг оси
вокруг оси 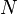 , и последним поворот на угол
, и последним поворот на угол 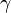 вокруг оси
вокруг оси 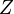 .
.
| |||||||||||||||||||
| Рассмотрим движение твердого тела, одна из точек которого во все время движения остается неподвижной. При таком движении все остальные точки тела движется по сферическим поверхностям, центры которых совпадают с неподвижной точкой. По этой причине рассматриваемое движение тела называется сферическим движением. Для определения положения тела в каждый момент времени воспользуемся двумя системами осей координат: неподвижной системой
Положение данного тела в пространстве будет вполне определено, если будет известно положение подвижной системы осей
Заданием углов При движении твердого тела, одна из точек которого остается неподвижной, эти углы непрерывно изменяются во времени, т.е.
Уравнения (4), однозначно определяющие сферическое движение тела, называются уравнениями сферического движения твердого тела. Для определения кинематических характеристик сферического движения тела (угловой скорости, скоростей его точек и т.д.) приведем теорему Эйлера-Даламбера (без доказательства): твердое тело, имеющее одну неподвижную точку, можно переместить из одного положения в любое другое поворотом вокруг некоторой оси, проходящей через неподвижную точку. Рассмотрим малый промежуток времени
Уменьшая величину промежутка времени Предел, к которому стремится отношение
Вектор мгновенной угловой скорости Линейная скорость точки
где - Из (6) следует, что модуль скорости точки
Вектор скорости точки Проекции скорости точки на неподвижные оси координат определяются по формулам Эйлера
Здесь: В заключении приводим уравнения мгновенной оси вращения в неподвижной системе осей
Рассмотрим несколько примеров. Пример 2. Твердое тело движется вокруг неподвижной точки
Найти в момент Решение. Найдем значения проекций угловой скорости при
Проекции скорости точки
Модуль скорости точки
По заданным проекциям угловой скорости найдем ее модуль
Из формулы (7) для расстояния от точки Пример 3. Конус с углом при вершине
Решение. Движение катящегося конуса является сферическим, так как его вершина Найдем расстояние
Модуль угловой скорости конуса определим по формуле (7)
Зная направление скорости Перейдем к определению скоростей точек Найдем расстояние
Воспользовавшись формулой (7), определяем скорость точки
Вектор скорости
| |||||||||||||||||||
Линейная скорость сферического движения.
Вращательное движение — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.
При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
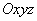 с началом в неподвижной точке
с началом в неподвижной точке 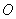 и подвижной системой
и подвижной системой 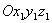 , неизменно связанной с твердым телом, с началом в той же точке
, неизменно связанной с твердым телом, с началом в той же точке 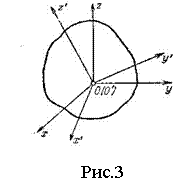
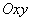 и подвижной плоскости
и подвижной плоскости 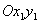 через
через 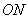 и установим на ней положительное направление (от
и установим на ней положительное направление (от 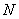 ); эта прямая
); эта прямая 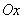 и линией узлов
и линией узлов  . Этот угол лежит, очевидно, в плоскости
. Этот угол лежит, очевидно, в плоскости 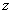 . Угол между осями
. Угол между осями 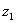 обозначим через
обозначим через 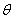 . Этот угол отсчитывается от оси
. Этот угол отсчитывается от оси 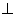 пл.
пл. 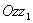 ). Угол между
). Угол между 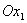 обозначим через
обозначим через 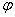 . Этот угол лежит в плоскости
. Этот угол лежит в плоскости 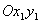 и отсчитывается от линии узлов против движения часовой стрелки, если смотреть с положительного конца оси
и отсчитывается от линии узлов против движения часовой стрелки, если смотреть с положительного конца оси 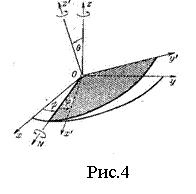
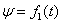 ,
, 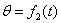 ,
, 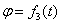
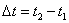 , за которое какая-нибудь точка твердого тела перемещается из положения
, за которое какая-нибудь точка твердого тела перемещается из положения 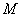 в положение
в положение  . При этом тело повернулось на угол
. При этом тело повернулось на угол 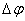 вокруг некоторой оси
вокруг некоторой оси 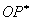 (рис.5).
(рис.5).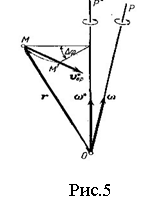
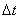 , получаем ряд положений оси
, получаем ряд положений оси 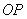 при
при 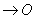 называется мгновенной осью вращения тела для данного момента времени.
называется мгновенной осью вращения тела для данного момента времени.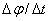 , когда
, когда 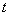
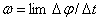
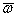 в данный момент откладывается по мгновенной оси
в данный момент откладывается по мгновенной оси 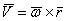
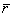 - радиус-вектор точки
- радиус-вектор точки 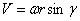 , где
, где 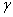 - угол между радиусом-вектором
- угол между радиусом-вектором 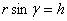 , где
, где  - расстояние от точки
- расстояние от точки 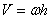
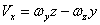 ,
,
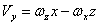 ,
,
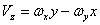
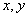 и
и 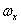 ,
, 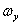 и
и 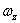 - проекции вектора угловой скорости
- проекции вектора угловой скорости 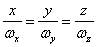
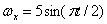 ,
, 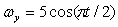 ,
, 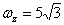 .
.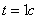 скорость точки
скорость точки 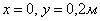 и
и 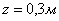 .
.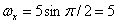 ,
, 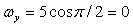 ,
, 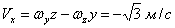 ,
,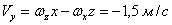 ,
,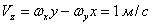 .
.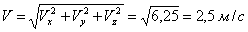 .
.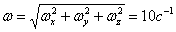 .
.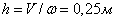 .
.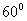 и радиусом основания
и радиусом основания 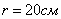 катится по неподвижной горизонтальной плоскости без скольжения. Скорость центра основания постоянна и равна
катится по неподвижной горизонтальной плоскости без скольжения. Скорость центра основания постоянна и равна 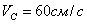 . Определить угловую скорость конуса
. Определить угловую скорость конуса  , а также скорости наинизшей и наивысшей точек основания
, а также скорости наинизшей и наивысшей точек основания 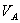 и
и 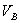 (рис.6).
(рис.6).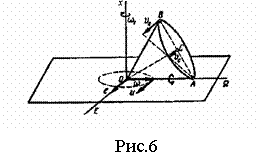
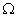 совпадает с образующей
совпадает с образующей 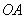 , по которой конус соприкасается с неподвижной плоскостью, так как скорости точек этой образующей равны нулю.
, по которой конус соприкасается с неподвижной плоскостью, так как скорости точек этой образующей равны нулю.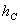 от точки
от точки 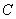 до мгновенной оси
до мгновенной оси 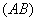
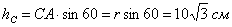 .
.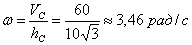 .
.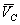 , откладываем от точки
, откладываем от точки  и
и 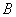 . Скорость точки
. Скорость точки 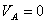 .
.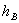 от точки
от точки 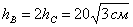 .
.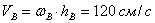 .
.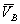 , так же как и
, так же как и 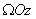 .
.