ИЗУЧЕНИЕ ОСНОВНОГО УРАВНЕНИЯ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА.

ИЗУЧЕНИЕ ОСНОВНОГО УРАВНЕНИЯ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА.

Цель работы:Изучение динамики вращательного движения, измерение момента инерции маятника Обербека.

Расчётные формулы:

Рабочая формула для расчета момента инерции маятника Обербека.

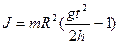
Расчет погрешности можно осуществить на основании формулы, считая, что в эксперименте реализована и процедура рандомизации, в результате которой систематические погрешности превращены в случайные:

D ,

где .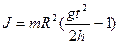

Найдем погрешность времени Dt:

t= ,

где t – среднее значение времени

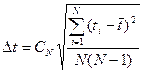
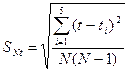
где N – число опытов (N=5), S_Nt – сумма N опытов по t, Относительная погрешность P₀ =0.8; Из таблицы “Коэффициенты стьюдента”, находим коэффициент соответствующий нашей относительной погрешности P₀: С_N=C₅=1,5 где С_N – это коэффициент стьюдента. В результате всех наших преобразований получаем формулу для расчета абсолютной погрешности времени:

Dt = C₅*S_Nt

Нахождение tga и его погрешности:

Использование функциональных шкал позволяет осуществить процедуру выравнивая графиков функций, в результате которой через экспериментальные точки можно провести прямую линию:

y=Ax+B;

Приведенное требование реализуется в методе наименьших квадратов, который позволяет найти наивероятнейшие значения параметров А и В:

А=tga=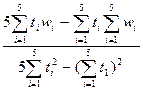

В=

Формулы для вычисления среднего квадратического отклонения экспериментальных точек от прямой S₀ и средних квадратичных отклонений коэффициентов А и В:

;

где n=5

;

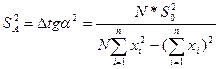где x_i=t_i, N=5.

на основании формулы: M=tga*J

получим формулу для решения погрешности момента силы:

DМ=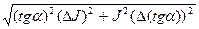

1. Измерения проводим используя малый шкив маятника:

R₁=0.009м; h=0.75м; g=9.81м/с²;
m=0.0658 кг;
T,c						t_ср,с	Dt
T,c	25,61	25,21	24,85	26,31	30,01	26,34	2,61
m=0.1216 кг;
T,c						t_ср,с	Dt
T,c	21,76	18,98	19,85	20,06	20,32	20,19	1,26

Найдем погрешность момента инерции:

Найдем погрешность времени t:

2. Проводим измерения используя большой шкив маятника:

R₁=0.017м; h=0.75м; g=9.81м/с²;
m=0.0658 кг;
T,c						t_ср,с	Dt
T,c	16,05	14,87	14,68	14,95	16,62	15,43
m=0.1216 кг;
T,c						t_ср,с	Dt
T,c	10,21	9,81	10,1	10,07	9,94		0,2

Найдем погрешность момента инерции:

Найдем погрешность времени t:

Определение зависимости момента инерции от расстояния грузов от оси вращения крестовины:

R=0.017 м; h=0.75 м; m=0.0659 кг.
r₁=0.18	r₂=0.17	r₃=0.16	r₄=0.15	r₅=0.14
T	T	T	T	T
11,65	10,85	10,3	10,53	10,61
11,33	10,63	10,78	10,67	10,74
11,12	10,4	10,73	9,94	10,16
11,3	11,79	10,93	10,07	9,78
10,61	11,32	10,49	10,47	9,69
t_ср

Вывод:

ü с увеличением расстояния между осью вращения и положением цилиндров, момент инерции маятника J увеличивается;

ü угловая скорость вращения маятника обратно пропорционально зависит от величины Dt, то есть чем меньше время прохождения расстояния h^’ , тем угловая скорость больше, иначе – меньше;

ü момент силы М, не зависит от положения цилиндров на крестовине и остается неизменным, то есть "х (М=const).