
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Маятник Максвелла
СПб ГУАП
КАФЕДРА № ___
Рейтинг за работу __________________________________________
Преподаватель Прилипко В.К.
ОТЧЕТ
о лабораторной работе по курсу
ОБЩАЯ ФИЗИКА
" Маятник Максвелла "
Работу выполнил
студент группы № 3127 КС Симаньков А.
_______________________
С-ПЕТЕРБУРГ
2011 г.
Цель работы:определение момента инерции маятника Максвелла.
Задание 1 – определить экспериментально момент инерции маятника.
1)Описание установки: Используемый в работе прибор содержит измерительную часть, включающую в себя миллисекундомер, измеряющий время падения маятника; колонну с нанесенной метрической шкалой. На колонне смонтированы два кронштейна: один (верхний) — неподвижный с воротком для крепления подвеса, электромагнитом для удержания маятника до начала эксперимента и фотодатчиком для сигнализации начала отсчета времени; другой кронштейн (нижний) — подвижный, со вторым фотоэлементом для сигнализации конца падения маятника.
Кнопка "Пуск" отключает электромагнит и запускает миллисекундомер, а кнопка "сброс" обнуляет показания секундомера, т.е. подготавливает прибор к следующему эксперименту.
Массу и момент инерции маятника можно изменять с помощью сменных колец, надеваемых на диск.
2) Методика выполнения и рабочие формулы: Маятник Максвелла представляет собой диск, жестко насаженный на стержень и подвешенный на двух тонких нерастяжимых нитях. Намотав нити на стержень, можно сообщить маятнику потенциальную энергию относительно нижнего положения, определяемого длиной нитей. Если маятник отпустить, то он начнет, вращаясь, падать вниз.
Принимая во внимание только консервативные силы, действующие на маятник, закон сохранения его энергии можно записать в виде:
(½) mV2 +( ½) Iw2 + mgh = mgh0 , (1)
где h0 — начальная высота подъема; h — текущая высота; m — масса маятника; I — момент инерции маятника относительно его оси; V — скорость центра масс; W — угловая скорость относительно своей оси; g — ускорение свободного падения.
Продифференцируем уравнение (1) по времени:
MV dV/dt + Iw dw/dt + mg dh/dt =0. (2)
Так как dV/dt = a , w = V/r , dh/dt = V, где а — ускорение центра масс, r — радиус стержня. Тогда уравнение (2) переписывается в виде:
mVa + Iva/r2 + mgV=0 (3) => I=mr2(-g/a-1) (4)
Так как ускорение а постоянно (из уравнения (4) , то: h0= - at2 , где t – время падения.
Тогда: I=mr2( gt2 / 2h0 -1) .
Таким образом измерив непосредственно t , h0 ,r , m , можно определить момент инерции маятника Максвелла.
3) Результаты измерений и вычислений: Результаты измерений занесены в таблицу №1.
Таб. №1
| Т1 М1 L1 | 0.801 | 0.797 | 0.794 | 0.795 | 0.811 | 0.796 | 0.805 | 0.795 | 0.781 | 0.788 |
| Т2 М2 L2 | 1.165 379.8 | 1.170 379.8 | 1.181 379.8 | 1.171 379.8 | 1.173 379.8 | 1.175 379.8 | 1.166 379.8 | 1.175 379.8 | 1.172 379.8 | 1.159 379.8 |
| Т3 М3 L3 | 1.208 513.4 | 1.203 513.4 | 1.201 513.4 | 1.211 513.4 | 1.197 513.4 | 1.211 513.4 | 1.209 513.4 | 1.192 513.4 | 1.2 513.4 | 1.201 513.4 |
4) Примеры расчетов:
Среднее время падения — среднее арифметическое величин из каждой серии опытов:
t1 = 0,796с;
t2 = 1.0707с;
t3 = 1.203 с;
Момент инерции в каждой серии опытов:
I1= 0,125 × (0,005) 2 (9,8×0.79612 / 2× 0,15 - 1) =2,8* 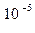 кг×м2
кг×м2
I2= 0,379 × (0,005) 2 (9,8× 1,07072 / 2× 0,15 - 1) = 1,5* 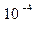 кг×м2
кг×м2
I3= 0,513 × (0,005) 2 (9,8× 1,2032 / 2× 0,15 - 1) = 2,6 * 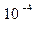 кг×м2
кг×м2
5) Расчет погрешности:
Погрешность измерения можно найти по формуле = |dI / dt| q t = mr2gt/h0(q t +t/2h0q h ) , где q t=0,001с — систематическая погрешность миллисекундомера, q h=0,0005м
q t 1= 0,125 × (0,005) 2 × 9,8 × 0,796/0,15(0,001+0,796/2 × 0,15 × 0,0005) = 3*  кг×м2
кг×м2
q t 2= 0,379 × (0,005) 2 × 9,8 × 1,0707/0,15(0,001+1,0707/2× 0,15 × 0,0005) = 9 *  кг×м2
кг×м2
q t 3= 0,513 × (0,005) 2 × 9,8 × 1,203/0,15(0,001+1,203/2 × 0,15 × 0,0005) = 1,25* 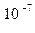 кг×м2
кг×м2
Задание 2 – определить теоретически момент инерции маятника.
Момент инерции стержня маятника относительно его оси равен
Ic = mcr2 , где mc = 33,0 г — масса стержня , r = 0,5 см — его радиус.
Ic = 0,033 × (0,005)2 = 8* 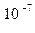 кг×м2
кг×м2
Момент инерции диска маятника относительно его оси равен
Iд = mд (R12 + r2), где mд = 125 г — масса диска , R1 = 3,8 см — его радиус.
Iд = 0,125 × (0,038)2 = 1,8* 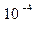 кг×м2
кг×м2
Момент инерции кольца от маятника относительно его оси равен
Iм = mм (R12 + R22), где mм = 125 г — масса кольца , R2 = 4,3 см — его радиус.
Iм1 = 0,125 × (0,043)2 = 2,5* 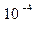 кг×м2
кг×м2
Iм2 = 0,379 × (0,043)2 = 7* 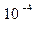 кг×м2
кг×м2
Iм3 = 0,513 × (0,043)2 = 9* 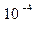 кг×м2
кг×м2
Момент инерции маятника равен I = Ic + Iд + Iм , т.о.:
I1 = 0,0000008 + 0,00018 + 0,00025 = 4,3* 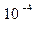 кг×м2
кг×м2
I1 = 0,0000008 + 0,00018 + 0,0007 = 8,8* 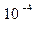 кг×м2
кг×м2
I1 = 0,0000008 + 0,00018+ 0,0009 = 1,08* 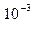 кг×м2
кг×м2
Средняя квадратичная погрешность определения периода Т колебаний маятника:
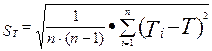
Для диска массой 125 грамм:
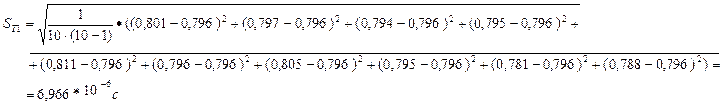 Для диска с кольцом массой 254,8 грамм:
Для диска с кольцом массой 254,8 грамм:
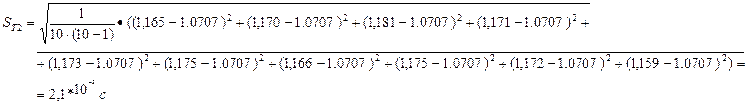 Для диска с кольцом массой 388,4 грамм:
Для диска с кольцом массой 388,4 грамм:
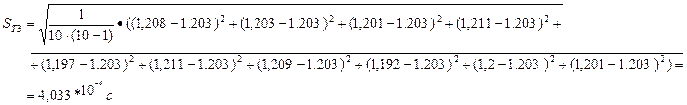
Суммарная погрешность определения периода колебаний Т:
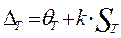 при n=10 k=1,5
при n=10 k=1,5
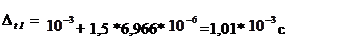
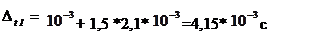
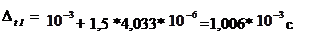
Вывод :Момент инерции маятника Максвелла равен:
I1 = 0,000028 кг×м2 , q t 1 = 3*  кг×м2 .
кг×м2 .
I2 = 0,00015 кг×м2 , q t 2 = 9 *  кг×м2 .
кг×м2 .
I3 = 0,00026 кг×м2 , q t 3 = 1,25* 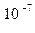 кг×м2 .
кг×м2 .
При этом более точный результат получился при измерении с самым легким кольцом.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|