Контакты

Случайная статья

Теория и расчет

⇐ ПредыдущаяСтр 3 из 3

Теория и расчет

Общая энергия 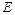колеса Максвелла массой 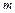и моментом инерции 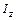состоит из потенциальной энергии 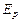, энергии поступательного движения 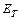и энергии вращения :

.

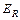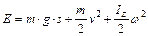где 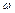- угловая скорость, 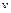- скорость поступательного движения, 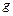- ускорение свободного падения, 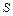- высота (со знаком минус)

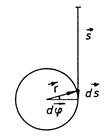
Рис. 3: Зависимость между увеличением угла 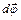и уменьшением высоты 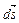в колесе Максвелла.

Рис. 4: Зависимость расстояния, пройденного точкой центра тяжести колеса Максвелла, от времени.

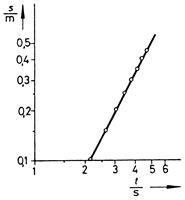
Из рис. 3

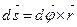
и

,

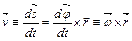где 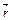- радиус вала.

В данном случае 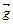параллелен 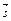, а 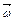перпендикулярен 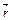, поэтому

.

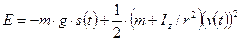Поскольку общая энергия 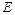постоянна с течением времени, дифференцирование приводит к

.

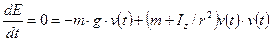Для 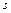( 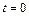) = 0 и v( 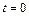) = 0 получаем

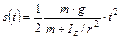(1)

и

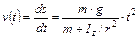(2)

Масс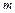а равна 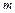= 0,436 кг. Радиус 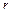вала равен 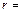2,5 мм.

Из графика на рис. 4 и функции

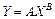
получаем

B = 1,99±0,01; A = 0,0196±0,0015 м/с²

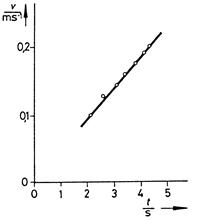
Рис. 5: Зависимость скорости центра тяжести колеса Максвелла от времени.

Из выражения (1) получаем момент инерции

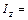9, 84 · 10^—⁴кгм².

Из графика на рис. 5 и функции

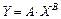
получаем

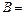1,03 ± 0,015 (см. (2))

Рис. 6: Зависимость энергии колеса Максвелла от времени:

1. Отрицательная потенциальная энергия

2. Поступательная энергия

3. Энергия вращательного движения

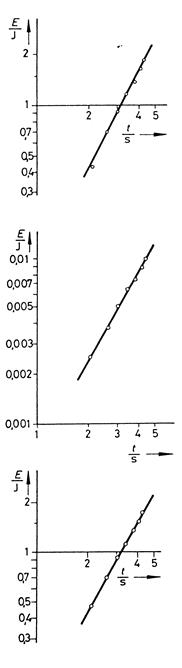
Как видно из рис. 6, что потенциальная энергия почти полностью переходит в энергию вращательного движения.

⇐ Предыдущая 1 23

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.