
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Цель работы: изучение особенностей и основных характеристик колебаний системы, состоящей из двух связанных маятников.
Цель работы: изучение особенностей и основных характеристик колебаний системы, состоящей из двух связанных маятников.
| К |
| ИП |

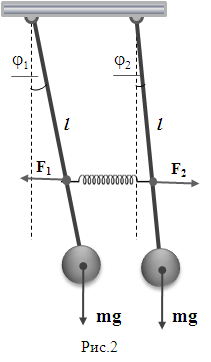 Оборудование.В комплект измерительной установки (рис.1) входят: два физических маятника, связанные cъемной легкой пружиной или жесткой перемычкой; источник питания ИП; аналогово-цифровой преобразователь «Кобра 3» К; измери-тельная рулетка; соединительные провода. Маятники состоят из легких металлических стержней, на конце которых укреплены массивные твердые тела. Расстояние от оси враще-ния до креплений пружины можно изменять в широких пределах. Колебания свя-занных маятников преобра-зуются с помощью «Кобра 3» в цифровой электричес-кий код, который обра-батывается специальной программой, а результат выводится на монитор в виде зависимости U(t). Измерения искомых вели-чин производят с помощью инструментов программы “Measture”.
Оборудование.В комплект измерительной установки (рис.1) входят: два физических маятника, связанные cъемной легкой пружиной или жесткой перемычкой; источник питания ИП; аналогово-цифровой преобразователь «Кобра 3» К; измери-тельная рулетка; соединительные провода. Маятники состоят из легких металлических стержней, на конце которых укреплены массивные твердые тела. Расстояние от оси враще-ния до креплений пружины можно изменять в широких пределах. Колебания свя-занных маятников преобра-зуются с помощью «Кобра 3» в цифровой электричес-кий код, который обра-батывается специальной программой, а результат выводится на монитор в виде зависимости U(t). Измерения искомых вели-чин производят с помощью инструментов программы “Measture”.
Рис. 1. Измерительная установка
- 3 -
Краткая теория
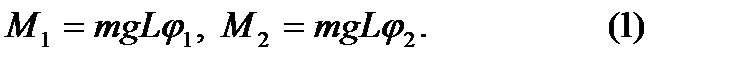 Колебательную систему, состоящую из двух или более взаимосвязанных физических (математических) маятников называют связанными маятниками. Рассмотрим простейшую колебательную систему (рис.2), состоящую из двух одинаковых физических маятников, соединенных между собой невесомой пружиной с небольшой жесткостью k. Расстояния от точки подвеса до центра масс грузов одинаковы и равны L, а расстояние от точки подвеса до крепления пружины – l. Колебания маятников в вертикальной плоскости будут описываться двумя незави-симыми параметрами – углами φ1 и φ2 их отклонения от вертикали. Полагаем, что моменты сил трения и сопротивления, действующие на маятники, ничтожно малы и ими можно пренебречь. Тогда на маятники будут действовать только моменты силы тяжести и силы упругости. Векторы моментов силы тяжести направлены вдоль оси вращения «от нас», а их модули при малых (в пределах sin φ ≈ φ) колебаниях соответ-ственно равны:
Колебательную систему, состоящую из двух или более взаимосвязанных физических (математических) маятников называют связанными маятниками. Рассмотрим простейшую колебательную систему (рис.2), состоящую из двух одинаковых физических маятников, соединенных между собой невесомой пружиной с небольшой жесткостью k. Расстояния от точки подвеса до центра масс грузов одинаковы и равны L, а расстояние от точки подвеса до крепления пружины – l. Колебания маятников в вертикальной плоскости будут описываться двумя незави-симыми параметрами – углами φ1 и φ2 их отклонения от вертикали. Полагаем, что моменты сил трения и сопротивления, действующие на маятники, ничтожно малы и ими можно пренебречь. Тогда на маятники будут действовать только моменты силы тяжести и силы упругости. Векторы моментов силы тяжести направлены вдоль оси вращения «от нас», а их модули при малых (в пределах sin φ ≈ φ) колебаниях соответ-ственно равны:
- 4 -
Модули сил упругости, приложенные к обоим маятникам, одинаковы (см. рис.2) и равны  а модули моментов силы упругости -
а модули моментов силы упругости -  (2)
(2)
Вектор момента силы упругости М1 направлен вдоль оси вращения «от нас», а вектор момента силы упругости М2 – «к нам», т.е. по направлению вектора углового перемещения φ2.
С учетом (1) и (2) основное уравнение динамики враща-тельного движения 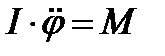 применительно к каждому маятнику для малых колебаний имеет вид:
применительно к каждому маятнику для малых колебаний имеет вид:
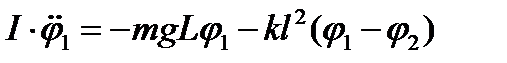 ,
,
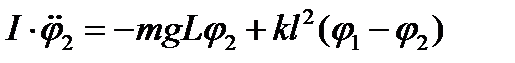 . (3)
. (3)
Систему уравнений (3) путем почленного сложения и вычита-ния уравнений с последующим делением на I и введением новых переменных 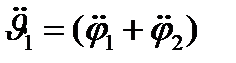 и
и  можно преобразовать к виду
можно преобразовать к виду
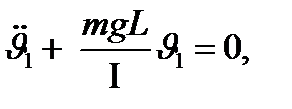
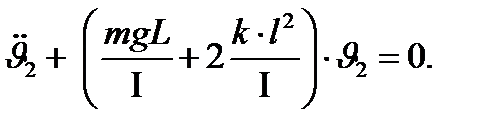 (4)
(4)
Полученные уравнения (4) являются уравнениями колебаний гармонических осцилляторов с собственными частотами
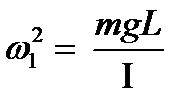 и
и 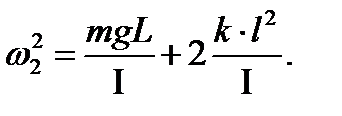 (5)
(5)
- 5 -
Общее решение уравнений (4) являются уравнения вида
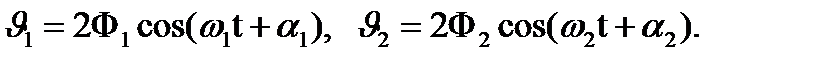
Для удобства амплитуды угловых перемещений обозна-чены 2F1 и 2F2, а начальные фазы - a1 и a2. Обратный переход к углам отклонения маятников позволяет установить зависимости φ1(t) и φ2(t):
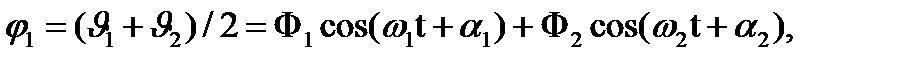
 (6)
(6)
Из уравнений (6) находим угловые скорости маятников:
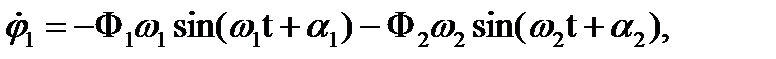
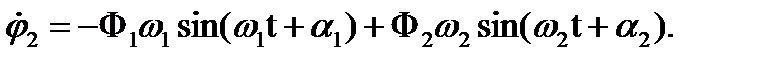 (7)
(7)
Таким образом, в общем случае колебания каждого маятника складываются из двух независимых колебаний с частотами w1 и w2, которые определяются выражениями (5) и носят название нормальных частот.
Как видно из уравнений (6), возможны случаи, когда оба маятника одновременно колеблются лишь с одной из нормальных частот (т.е. при Ф1=0 или Ф2=0). Каждая из возможностей осуществляется в зависимости от способа возбуждения колебаний в системе, т.е. от начальных условий (t=0). Начальные отклонения и угловые скорости маятников из (6) и (7) имеют вид:
- 6 -

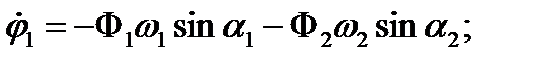
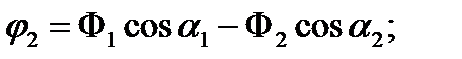
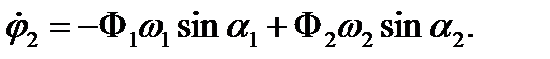 (8)
(8)
Из уравнений (8) вытекают следующие выводы.
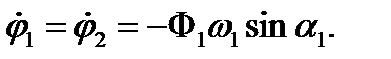 1. Когда Ф2=0, то в начальный момент оба маятника были откло-нены на один и тот же угол φ10= φ20=Ф1cosa и имели одинаковые скорости
1. Когда Ф2=0, то в начальный момент оба маятника были откло-нены на один и тот же угол φ10= φ20=Ф1cosa и имели одинаковые скорости
Этот случай соответствует так называемым синфазным колеба-ниям. Для получения синфазных колебаний маятники соединяют жесткой невесомой рейкой. Так как момент инерции связанных маятников увеличивается, то оба маятника колеблются с меньшей из нормальных частот w1.
2. Случай Ф1=0 означает, что в начальный момент маятники были отклонены в противоположные стороны  и имели противоположные скорости
и имели противоположные скорости  При таком способе возбуждения оба маятника колеблются в противофазе с большей из нормальных частот w2.
При таком способе возбуждения оба маятника колеблются в противофазе с большей из нормальных частот w2.
3. В общем случае произвольного способа возбуждения, каждый из маятников осуществляет сложное колебание, характер которого удобно наблюдать при слабой связи между маятниками: kl2<<mgL. Тогда разность Dw = w2 - w1 мала по сравнению с нормальными частотами и периодическое возрастание и убывание амплитуды колебаний каждого маятников происходит с частотой Dw. Такие колебания называют биениями.
- 7 -
На рисунке 3 приведены биения связанных маятников для расстояния от оси вращения до крепления пружины l=30 см. На зависимости U(t) отрезок времени между соседними узлами (или пучностями) является периодом биений Тб. По периоду биений определим их циклическую частоту: Dw= 2π/ Тб. (9)
| Тб |
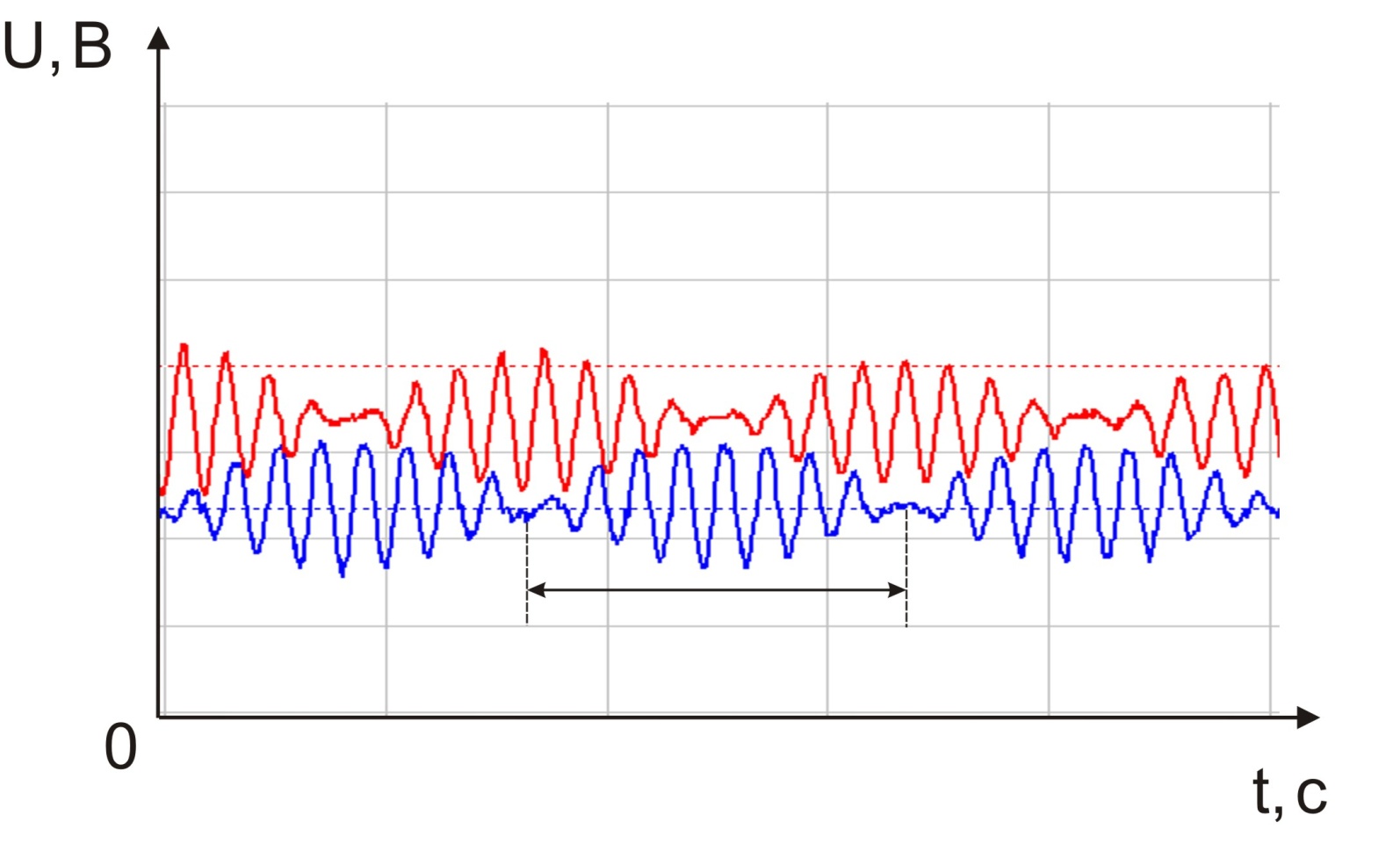
Рис.3. График биений.
Как следует из уравнений (5) изменение расстояния l от оси вращения до точки крепления пружины приведет к изменению циклической частоты w2, а следовательно, и к изменению периода биений Тб.
Выполнение работы
Задание 1. Исследование синфазных и противофазных колебаний связанных маятников.
1. Установите одинаковую длину связанных маятников (длина измеряется рулеткой).
2. Включите аппаратуру измерительной установки и персональ-ный компьютер.
- 8 -
3. Вызовите программу «Measura» и в открывшемся окне установите необходимые для измерений опции.
4. Снимите соединительную пружину и измерьте для каждого маятника время t1 и t2 n=10-20 колебаний, измерения повторите несколько раз и вычислите периоды Т1 и Т2 свободных колебаний.
5. По средним значениям периодов определите циклические частоты  и
и  колебаний маятников.
колебаний маятников.
6. На определенном расстоянии от оси вращения соедините маятники жесткой перемычкой. Измерьте для каждого маятника время t1 и t2 n=10-20 колебаний, измерения повторите несколько раз и вычислите периоды Т1 и Т2 синфазных колебаний.
7. По среднему значению периода определите циклическую частоту w колебаний связанных маятников.
8. Вместо жесткой перемычки установите легкую пружину и повторить пункты 7,8 для колебаний связанных маятников
«в противофазе».
9. Результаты измерений и вычислений занесите в таблицу 1.
Таблица 1.
| № п/п | n | t1 | T1 | t2 | T2 | w1 | w2 | n | tc | Tc | wc | n | tп | Тп | wп |
| - | с | с | с | с | с-1 | с-1 | - | с | с | с-1 | - | с | с | с-1 | |
| : | |||||||||||||||
| Ср. |
- 9 -
10. Сравните полученные значения циклических частот синфазных и противофазных колебаний с циклической частотой свободных колебаний каждого маятника. По проделанному заданию сделайте вывод.
Задание 2. Исследование биений связанных маятников.
1. Установить первое значение расстояния l1 от оси вращения до крепления пружины.
2. Придерживая перед пуском один и отклонив другой маятник, добиться возникновения биений связанных маятников.
3. Измерить несколько раз период Т1 биений связанных маятников и по его среднему значению вычислить циклическую частоту Dw.
4. Повторить пункты 2,3 для нескольких расстояний l.
5. Результаты измерений и вычислений занести в таблицу 2.
Таблица 2.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| l, см | |||||||||
| Тб, с | |||||||||
| Dw, с-1 |
6. Построить график зависимости частоты биений от длины Dw(l). По выполненному заданию сделать вывод.
- 10 -
Контрольные вопросы
1. Какие силы и моменты сил действуют на каждый маятник? Укажите их направления.
2. Приведите дифференциальные уравнения, описывающие колебания связанных маятников, и их решения.
3. Что понимают под нормальными частотами связанных маятников?
4. Какие колебания связанных маятников называются синфазными, противофазными?
5. Какие колебания связанных маятников называются биениями?
При каких условиях они возникают?
Рекомендуемая литература
1. СавельевИ.В. Курс физики. Т2. М.: Наука. 1989. §§66,70.
2. Трофимова Т. И. Курс физики. М.: Высшая школа. 1997. §§ 143, 146.
3. Ахматов А.С. и др. Лабораторный практикум по физике. М.: Высшая школа. 1980. Стр.181.
4. Инструкция по эксплуатации оборудования фирмы “PHYWE”.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ФИЗИКИ
Лаборатория
«Инновационные технологии обучения физике и КСЕ»
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|