Векторное пространство. Координаты вектора.

Векторное пространство. Координаты вектора.

Рассмотрим непустое множество элементов, которые будем обозначать через x, y, z, и множество действительных чисел. На этом множестве введем две операции (сложение и умножение). Пусть эти две операции подчиняются аксиомам:

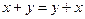
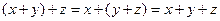
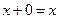
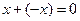
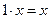
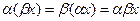
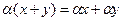
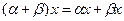
V; x, y, z, … 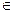V

Множество V с двумя операциями, удовлетворяющее аксиомам называется линейным пространством.

Элементы линейного пространства называются векторами, обозначаются 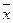, , 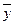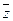. Существует единственный нулевой элемент, для каждого элемента существует единственный противоположный.

Размерность и базис линейного пространства. Пусть система n векторов линейно-независима, а любая система n+1 векторов – линейно-зависима, тогда число n называют размерностью пространства. dimV=n

Система этих n линейно-независимых векторов называется базисом линейного пространства. Рассмотрим систему n+1 векторов.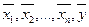

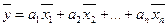
Такое представление называется разложение 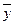по базису, а числа 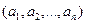называют координатами вектора.

Разложение любого вектора в выбранном базисе - единственно.