
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Ход работы
(2)
При смещении тела на величину X вдоль вертикали на него будет действовать сила:
(3)
Направленная к положению равновесия (в сторону обратную смещению)
Уравнение движения тела будет иметь вид:
(4)
Откуда:
(5)
где 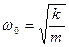 -круговая частота колебаний.
-круговая частота колебаний.
Период их:
(6)
Написанные уравнения характеризуют незатухающее гармоническое колебательное движение.
В случае наличия сил сопротивления, действующих на тело, колебания будут затухать. При малых скоростях движения тела, силу сопротивления 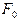 можно считать пропорциональной скорости движения:
можно считать пропорциональной скорости движения:
(7)
где 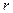 -коэффициент сопротивления среды.
-коэффициент сопротивления среды.
Уравнение движения тела в данном случае имеет вид:
(8)
а закон движения:
(9)
где 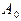 -начальная амплитуда;
-начальная амплитуда; 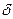 -коэффициент затухания;
-коэффициент затухания;
(10)
Амплитуда колебаний убывает по экспоненциальному закону.
Отношение амплитуд колебаний, соответствующих двум моментам времени, отличающихся друг от друга на период называют декрементом затухания:
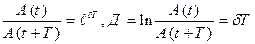
Амплитуда двух последующих колебаний обычно мало отличаются друг от друга, поэтому для более точного определения логарифмического декремента затухания измеряют амплитуды, отстоящие друг от друга на  периодов. Логарифмический декремент затухания в этом случае находится из формулы:
периодов. Логарифмический декремент затухания в этом случае находится из формулы:
(11)
где 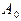 и
и 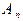 -амплитуды начального и конечного колебаний.
-амплитуды начального и конечного колебаний.
Колебания, которые совершаются за счет работы периодически меняющиеся внешней силы, называют вынужденными.
Пусть на тело действует внешняя сила, изменяющуюся по гармоническому закону с частотой 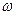 , сила сопротивления пропорциональная скорости тела и упругой силе. Напишем уравнение движения тела:
, сила сопротивления пропорциональная скорости тела и упругой силе. Напишем уравнение движения тела:
(12)
где 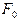 -амплитудное значение вынуждающей силы, при этом:
-амплитудное значение вынуждающей силы, при этом:
(13)
где 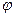 -сдвиг фаз между колебаниями системы и колебаниями внешней силы.
-сдвиг фаз между колебаниями системы и колебаниями внешней силы.
То есть, тело будет совершать гармоническое колебательное движение с частотой внешней силы.
Амплитуда колебания:
(14)
где 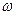 -частота собственных колебаний системы;
-частота собственных колебаний системы; 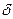 -показатель затухания.
-показатель затухания.
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний называется резонансом. Частота вынуждающей силы, при которой возникает резонанс, называется резонансной частотой  , а величина максимальной амплитуды называется резонансной амплитудой
, а величина максимальной амплитуды называется резонансной амплитудой 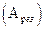 .
.
Из формулы (14)можно получить:
(15)
(16)
Для маятников с массами 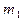 и
и 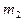 будем иметь:
будем иметь:
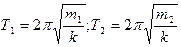
Откуда:
 (17)
(17)
Для более точного определения периода колебаний будем измерять время 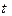 , за которое совершается
, за которое совершается 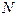 полных колебаний. Тогда:
полных колебаний. Тогда:
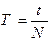 (18)
(18)
Ход работы
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|