Плоская система произвольно расположенных сил

4. Плоская система произвольно расположенных сил

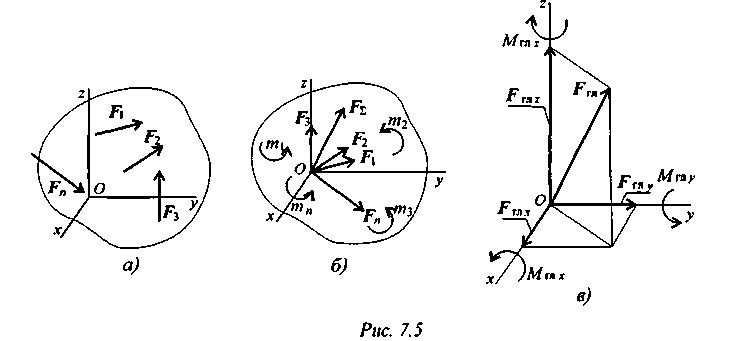
Теорема Лемма: Не изменяя действия силы на твердое тело, ее можно переносить параллельно самой себе в любую точку, добавляя при этом пару, момент которой равен моменту данной силы относительно новой точки приложения.

Теорема Пуансо

Произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы и пары сил. Сила равна главному вектору системы сил и приложена в произвольной точке (центре приведения), момент пары равен главному моменту системы сил относительно этой точки.

Главный вектор системы сил

Главный момент системы сил

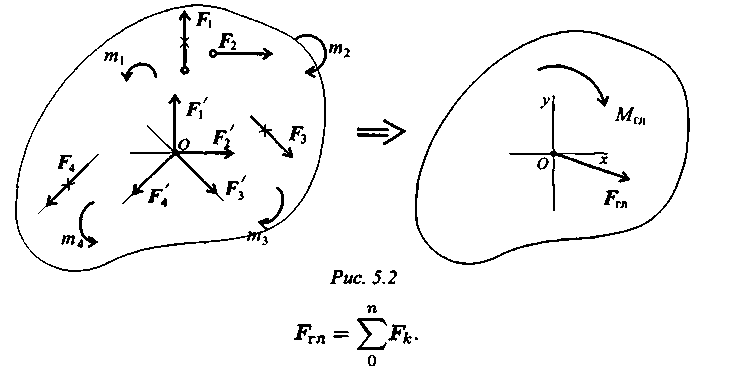
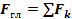
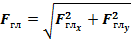
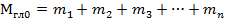
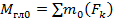
Влияние точки приведения

При изменении положения точки приведения величина главного вектора не изменится.

Величина главного момента при переносе точки приведения изменится, т. к. меняются расстояния от векторов - сил до новой точки приведения.

Произвольная плоская система сил может быть заменена одной силой, равнодействующей системы сил 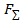. Численно равнодействующая равна главному вектору системы сил, но приложена в другой точке, относительно которой главный момент равен нулю.

;

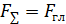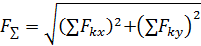
Точку приложения равнодействующей определяют по формуле

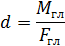
где d— расстояние от выбранной точки приведения до точки приложения равнодействующей.

Условие равновесия произвольной плоской системы сил

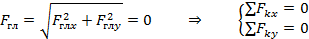
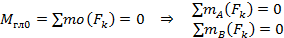
где А и В — разные точки приведения.