Плоская система сходящихся сил

2. Плоская система сходящихся сил

-система сил, линии действия которых лежат в одной плоскости и пересекаются в одной точке.

Задачу равновесия данной системы решают геометрическим или аналитическим способами.

Геометрический способопределения равнодействующей сходящихся сил:

· правило параллелограмма сил,

· правило треугольника сил.

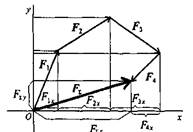
Силовой многоугольник – фигура, образованная векторами сил системы, в которой начало следующей силы совпадает с окончанием предыдущей.

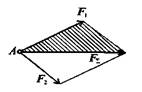
Построение силового многоугольника

1.Векторы сил системы вычерчивают в определенном масштабе:

- Один за другим в произвольной последовательности так, чтобы конец предыдущего вектора совпадал с началом последующего.

При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры, но на результат порядок вычерчивания не влияет.

- Стороны многоугольника должны быть параллельны соответствующим векторам сил.

2.Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего.

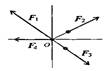
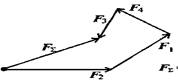
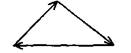
Геометрическое условие равновесия

Плоская система сходящихся сил находится в равновесии, если многоугольник сил этой системы замкнут.

Аналитический способопределения равнодействующей сходящихся сил:

Равнодействующую сходящихся сил определяют аналитическим способом с помощью метода проекций:

F_к_x= F sinα, F_к_y= F cos α

При геометрическом построении

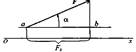
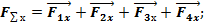
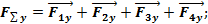
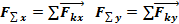
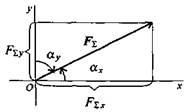
F_∑=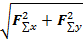

сos α_x =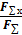

Аналитическое условие равновесия

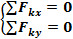
Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.