
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Метод контурных токов. Баланс активных и реактивных мощностей. Уравнения Кирхгофа в дифференциальных и комплексных формах. Топографическая диаграмма напряжений и векторная диаграмма токов
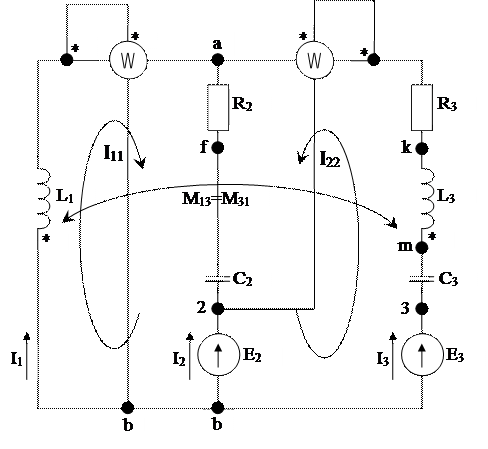 |
Дано: R1 = 0 Ом R2 = 75 Ом R3 = 69 Ом
L1 = 31 мГн L2 = 0 мГн L3 = 47 мГн
C1 = 0 мкФ C2 = 14 мкФ C3 = 48 мкФ
E1 = 0 B E2 = 255 В E3 = 249 В
φ1 = 0° φ2 = 219° φ3 = 39°
n = 50 Гц
w = 314 Гц
Найдем собственные сопротивления:
ХL1 = wL1 = 314 * 31*10-3 = 9,734 Ом
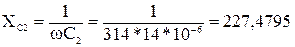 Ом
Ом
ХL3 = wL3 = 314 * 47*10-3 = 14,758 Ом
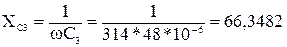 Ом
Ом
Собственные ЭДС контуров:
Ė2 = E2 * cosφ2 + j E2 * sinφ2 = 255 * cos219˚ + j 255 * sin219˚ =
= – 198,17 – j 160,48 B
Ė3 = E3 * cosφ3 + j E3 * sinφ3 = 249 * cos39˚ + j 249 * sin39˚ =
= 193,5 + j 156,7 B
Метод контурных токов
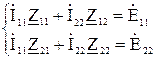
Найдем комплексные значения собственных и смежных сопротивлений и собственных ЭДС контуров:
Z11 = R2 + j(XL1 – XC2) = 75 + j(9,734 – 227,4795) = 75 – j 217,75 Ом
Z22 = R2 + R3 + j(– XC2 + ХL3 – XC3) = 75 + 69 + j(– 227,4795 + 14,758 – 66,3482) =
= 144 – j 279,07 Ом
Z12 = Z21 = R2 – jXC2 = 75 – j 227,48 Ом
Ė11 = – Ė2 = 198,17 + j 160,48 B
Ė22 = – Ė2 + Ė3 = 198,17222 + j 160,4767 + 193,50934 + j 156,70078 =
= 391,68 + j 317,18 B
(75 – j 217,7455) * İ11 + (75 – j 227,4795) * İ22 = 198,17222 + j 160,4767
(75 – j 227,4795) * İ11 + (144 – j 279,0697) * İ22 = 391,68156 + j 317,17748
Составим расширенную матрицу сопротивлений и ЭДС, решив которую найдем контурные токи:
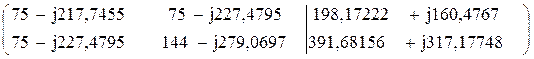
İ11 = – 1,4305 – j 1,8557 A
İ22 = 0,9744 + j 2,7978 A
Истинные токи в ветвях будут:
İ1 = İ11 = – 1,4305 – j 1,8557 = 2,34 ej52,37 A
İ2 = – İ11 – İ22 = 1,4305 + j 1,8557 – 0,9744 – j 2,7978 = 0,4561 – j 0,9421 =
= 1,046 ej64,17 A
İ3 = İ22 = 0,9744 + j 2,7978 = 2,96 ej70,8 A
Найдем показания ваттметров:
Для этого найдем напряжение Uab и Ua2
Uab = – İ2 (R2 – j XC2) = (– 0,4561 + j 0,9421) * (75 – j 227,4795) = – 34,2075 +
+ j 103,7534 + j 70,6575 + 214,308437 = 180,100937 + j 174,4109 B
Ua2 = Uab – Ė2 = 180,100937 + j 174,4109 + 198,17222 + j 160,4766997 =
= 378,273157 + j 334,8875997 В
PW1 = Re [Uab * I1] = Re [(180,100937 + j 174,4109) * ( – 1,4305 + j 1,8557)] =
= Re [– 257,6343904 + j 334,2133088 – j 249,4947925 – 323,6543071] =
= –581,29 Вт
PW2 = Re [Ua2 * I3] = Re [(378,273157 + j 334,8875997) * (0,9744 – j 2,7978)] =
= Re [368,5893642 – j 1058,332639 + j 326,3144771 + 936,9485264] =
= 1305,54 Вт
Баланс активных и реактивных мощностей
Для того чтобы найти активную и реактивную мощности, найдем сначала полную мощность.
Sпр = Sист
Sпр = S1 + S2 + S3
Sист = Ė2İ2 + Ė3İ3
S1 = İ12 * j XL1 = (– 1,4305 – j 1,8557)2 * j 9,734 = – 51,67934 – j 13,60124 BA
S2 = İ22 * (R2 – j XC2) = (0,4561 – j 0,9421)2 * (75 – j 227,47953) =
= – 246,45657 + j 90,124299 BA
S3 = İ32 * (R3 +j (XL3 – XC3)) = (0,9744 + j 2,7978)2 * (69 – j 51,59019533) =
= – 193,30993 + j 731,06156 BA
Sпр = –51,67934 –j 13,60124 –246,45657 + j 90,124299 – 193,30993 + j 731,06156 =
= – 491,4458 + j 807,5846 ВА
Sист = (– 198,17222 – j 160,4766997) * (0,4561 – j 0,9421) + (193,5093444 +
+ j 156,7007774) * (0,9744 + j 2,7978) = – 491,4334 + j 807,5943 BA
P = Re [S]
Pпр = Pист следовательно Re [Sпр] = Re [Sист]
Re [Sпр] = – 491,4458 Вт
Re [Sист] = – 491,4334 Вт
Q = Im [S]
Qпр = Qист следовательно Im [Sпр] = Im [Sист]
Im [Sпр] = 807,5846 ВАР
Im [Sист] = 807,5943 ВАР
Таким образом, можно сказать, что баланс активных и реактивных мощностей сходится.
Уравнения Кирхгофа в дифференциальных и комплексных формах
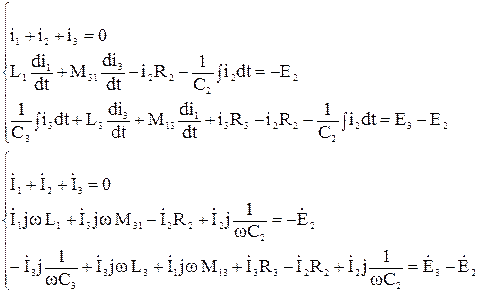
Топографическая диаграмма напряжений и векторная диаграмма токов
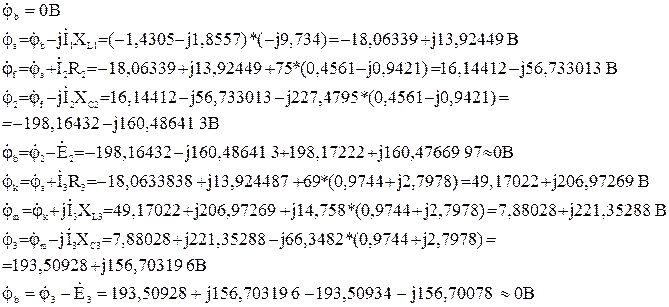
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|