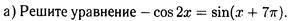- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Найти область определения функции .
Вариант 1
№1. Найти область определения функции 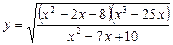 .
.
№2. Упростить выражение 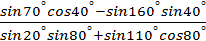 .
.
№3. Решить уравнение и неравенство: а) 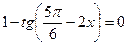 , б)
, б) 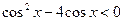 .
.
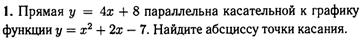 №4.
№4.
| |
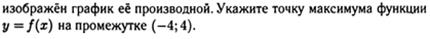 б)
б)
| |
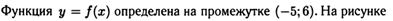
№5. Дана функция 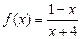 . К ее графику проведена касательная mв точке с абсциссой
. К ее графику проведена касательная mв точке с абсциссой 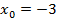 . Составить уравнение этой касательной m. Существует ли касательная к графику f(x), отличная
. Составить уравнение этой касательной m. Существует ли касательная к графику f(x), отличная
от m и параллельная m? Если существует, найдите ее уравнение.
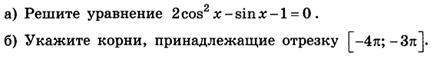 №6
№6
№7. а) Исследовать функцию 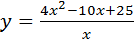 на монотонность и экстремумы.
на монотонность и экстремумы.
б) Найти наименьшее и набольшее значения функции на отрезке 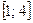 .
.
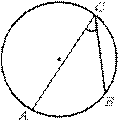
№8. В треугольнике ABC угол B равен 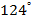 , AD – биссектриса угла A, угол C меньше угла ADB
, AD – биссектриса угла A, угол C меньше угла ADB
в 2,5 раза. Найдите градусную меру угла C.
№9. В основании прямой призмы лежит ромб с диагоналями 18 и 24. Площадь поверхности призмы равна 642. Найдите боковое ребро призмы.
№10.
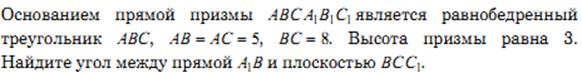
Вариант 2
№1.Найти область определения функции .
№2. Упростить выражение 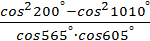 .
.
№3. Решить уравнение и неравенство: а) 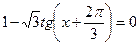 , б)
, б) 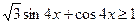 .
.
 №4.
№4.
| |
 а)
а)

| |
№5. Каково взаимное расположение касательной к графику функции 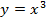 в точке с абсциссой
в точке с абсциссой 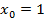
и прямой 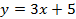 ?
?
 |
№6.
№7. а) Исследовать функцию 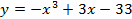 на монотонность и экстремумы.
на монотонность и экстремумы.
б) Найти наименьшее и наибольшее значения функции на отрезке 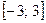 .
.
№8. В треугольнике АВС угол А равен 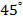 , угол В равен
, угол В равен 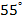 . Высоты треугольника АD и ВE пересекаются в точке О. Найдите градусную меру угла AOB.
. Высоты треугольника АD и ВE пересекаются в точке О. Найдите градусную меру угла AOB.
№9. Боковое ребро правильной четырехугольной пирамиды равно 15, а сторона основания – 18.
Найдите площадь поверхности пирамиды.
№10.

Вариант 3.
- Найти область определения функции
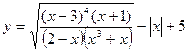 .
. - Упростить выражение
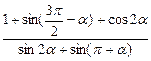 .
. - Решить уравнение и неравенство: a)
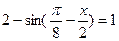 , б)
, б) 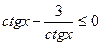 .
. - а) Точка движется по прямой. Зависимость ее координаты от времени задана формулой
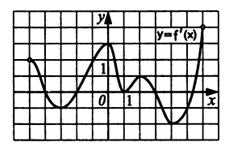
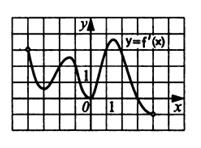
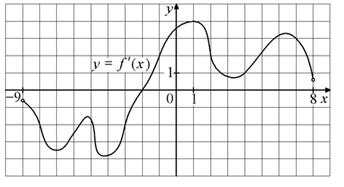
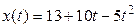 . Найдите момент времени t, когда тело остановится. б) На рисунке изображен график производной функции
. Найдите момент времени t, когда тело остановится. б) На рисунке изображен график производной функции 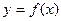 , определенной на интервале
, определенной на интервале 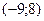 . Найдите точку экстремума функции на отрезке
. Найдите точку экстремума функции на отрезке 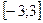 и укажите ее тип.
и укажите ее тип.
- Напишите уравнение касательной к графику функции
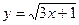 , параллельной прямой
, параллельной прямой 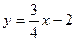 .
.

- а) Исследовать функцию
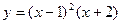 на монотонность и экстремумы. б) Найти наибольшее и наименьшее значения функции на отрезке
на монотонность и экстремумы. б) Найти наибольшее и наименьшее значения функции на отрезке 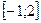 .
.
|
- Площадь боковой поверхности цилиндра равна 12π, а диаметр основания равен 6. Найдите высоту цилиндра
- Дана правильная четырехугольная пирамида МАВСD, ребра основания которой равны 52. тангенс угла между прямыми DM и AL равен 2. L середина ребра МВ. Найдите высоту пирамиды.
Вариант 4.
- Найти область определения функции
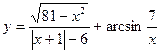
- Упростить выражение
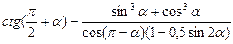
- Решить уравнение и неравенство: а)
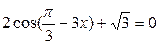 , б)
, б) 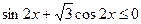 .
.
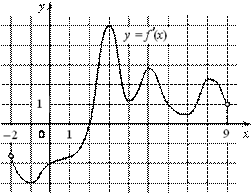
| а)На рисунке изображен график производной функции  , определенной на интервале , определенной на интервале 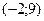 .В какой точке на отрезке .В какой точке на отрезке 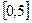 .функция .функция 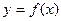 принимает свое наименьшее значение.
б) Прямая, проходящая через точку (3;-1), касается графика функции принимает свое наименьшее значение.
б) Прямая, проходящая через точку (3;-1), касается графика функции 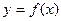 в точке (4;-2). Найдите в точке (4;-2). Найдите 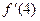 . .
|
- Написать уравнение той касательной к графику функции
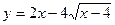 , которая составляет угол
, которая составляет угол 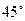 с осью ординат.
с осью ординат.
 |
- а) Исследовать функцию на монотонность и экстремумы
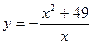
 б) Найти наибольшее и наименьшее значения этой функции на отрезке
б) Найти наибольшее и наименьшее значения этой функции на отрезке 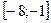 .
.
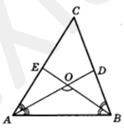
- Окружность вписана в равнобедренную трапецию, основания которой 18 и 50. Найдите радиус этой окружности. В треугольнике АВС угол С равен 580, биссектрисы АD и ВЕ
пересекаются в точке О. Найдите угол АОВ. Ответ дайте в градусах.

| Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 102. Найдите образующую конуса |
- В правильном тетраэдре АВСД точка Е середина ребра ВД. Найдите синус угла между прмой АЕ и плоскостью АВС.
Вариант 5
№1. Найти область определения функции 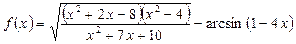 .
.
№2. Упростить выражение: 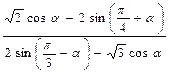 .
.
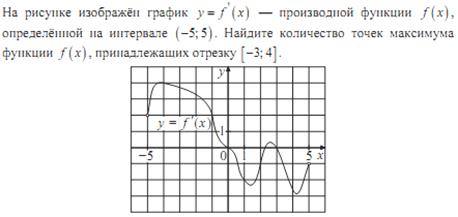 №3. Решить уравнение и неравенство: а)
№3. Решить уравнение и неравенство: а) 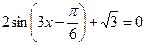 , б)
, б) 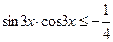 .
.
№4. а)
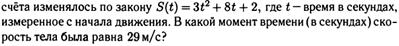
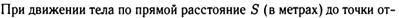 б)
б)
№5 Касательная к графику функции 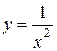 параллельна прямой
параллельна прямой 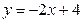 .
.
Определите абсциссу точки касания.
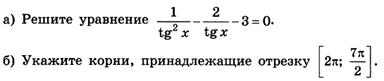 |
№6.
№7 а)Исследуйте функцию на монотонность и экстремумы 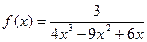
б) Найдите наибольшее 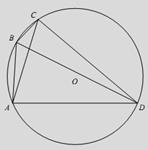 и наименьшее значения функции на
и наименьшее значения функции на 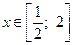 .
.

№8
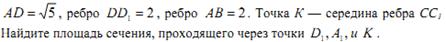
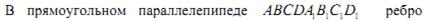 №9.
№9.
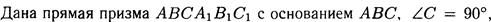
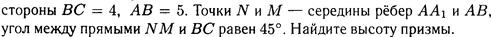 №10.
№10.
Вариант 6
№1. Найти область определения функции 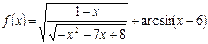 .
.
№2. Упростить выражение: 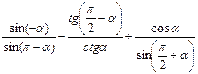
№3. Решить уравнение и неравенство: а) 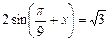 , б)
, б) 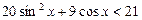 .
.
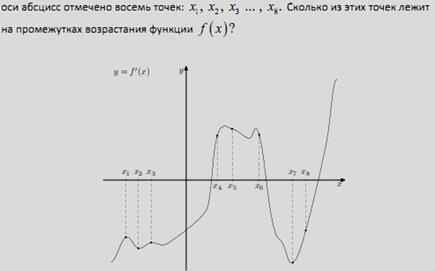
 №4. а)
№4. а)
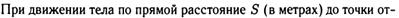
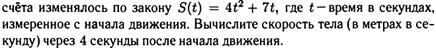 б)
б) 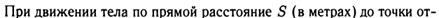
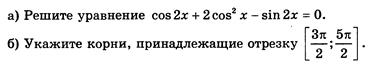 №5 Написать уравнения касательных к кривой
№5 Написать уравнения касательных к кривой 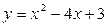 , проходящих через точку
, проходящих через точку 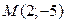 .
.
№6
№7 а)Исследуйте функцию на монотонность и экстремумы 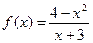
б) Найдите наименьшее значения функции на 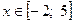 . .
. .
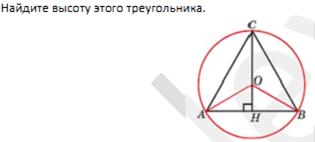
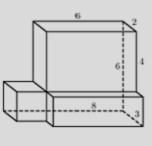
 №8
№8
 | |||
 | |||
 №9.
№9.
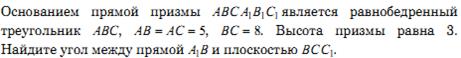 №10.
№10.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|