Хелпикс

Главная

Контакты

Случайная статья



Рабочий лист.



Рабочий лист.

Предмет Математика
Группа № 5 2 курс
Тема урока   Вычисление координаты середины отрезка и длины векторов по координатам.
ФИО преподавателя Тимиршина Алия Мунзиловна

Где находится задание:
Учебник М.И. Башмаков Математика, задачник, 2017г
Ссылка http://www.belgtis.ru/images/obuch/pm/MatematikaZadachnikBashmakov.pdf
Сроки выполнения задания 16.09.2020 до 17:00
Как выполнять задание Написать конспект по видео и продолжить запись по материалу, выполнить домашнее задание.
Домашняя работа По задачнику М.И. Башмакова на стр.114 №5.45
Обратная связь Выполненные работы отправить личным сообщением ВК
Как узнать отметку о выполненном задании Оценки будут выставлены в личный журнал преподавателя и отправлены в беседу ВК.

 Тема: Вычисление координаты середины отрезка и длины векторов по координатам.

Сегодня вы познакомитесь с формулами вычисления координат середины отрезка, вычисления длины отрезка по его координатам и вычисления расстояния между двумя точками.

Такие же задачи вы уже решали на плоскости. Сейчас же рассмотрим их в пространстве.

Итак, первым рассмотрим правило вычисления координат середины отрезка.

Отметим в прямоугольной координатной плоскости Охуz точку А с координатами x1, y1 и z1, а также точку B с координатами x2, y2 и z2. Отметим точку C, которая является серединой отрезка АB.

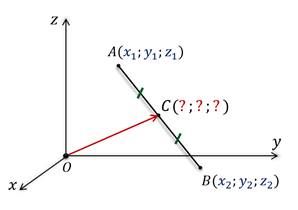
Можно записать, что вектор .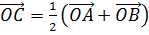

Действительно, ведь с одной стороны по правилу треугольника 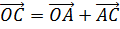, а с другой стороны .

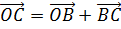Сложим покомпонентно эти равенства. Справа видим сумму противоположных векторов 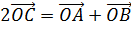, она равна нулю. Отсюда получаем, что вектор .

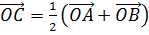Векторы ОА и ОB являются радиус-векторами точек А и B соответственно. Отсюда запишем их координаты.

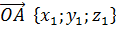
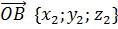
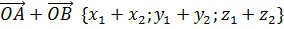
Равенство, выражающее вектор ОC через векторы ОА и ОB, запишем в координатах.

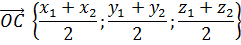
Получим такие координаты для вектора C. Но так как он является радиус-вектором точки C, то очевидно, что точка С будет иметь такие же координаты.

Можем сделать вывод, что каждая координата середины отрезка равна полусумме соответствующих координат его концов.

Задание: точка М середина отрезка АВ. Найти координаты точки М по координатам точек А и В.

Решение:

Мы рассмотрели примеры применения формул координат середины отрезка, а теперь перейдём к следующему виду задач: вычисление длины вектора по его координатам.

Длина вектора равна корню квадратному из суммы квадратов его координат.

Докажем это утверждение.

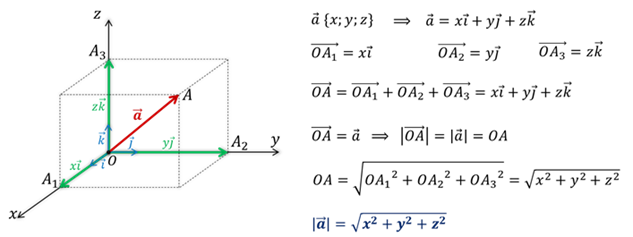
Что и требовалось доказать.

Задание: по координатам точек А и В найти длину вектора АВ.

а) , ;

б) , .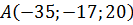

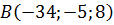Решение:

Задание: Вычислить длины векторов 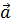, , 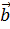, 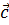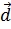и .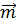

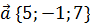
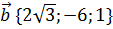
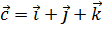
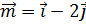
Решение:

Домашнее задание: По задачнику М.И. Башмакова на стр.114 №5.45
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.