ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА алгебры

ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА алгебры

(продолжительность урока-60 минут)

№ п/п	Этап урока	Формы работы
1.	Тема урока:Использование ограниченности функции. Использование монотонности и экстремумов функции.	1. Запиши в тетрадь число и тему урока. Классная работа. Использование ограниченности функции. Использование монотонности и экстремумов функции.
2.	Закрепление изученного материала:	1. Прочитайте параграфы13.3-13.4 Использование ограниченности функций, Использование монотонности и экстремумов функции. 2. Рассмотрите примеры из параграфов 3. Посмотрите видео по ссылке: https://www.youtube.com/watch?time_continue=615&v=zmh3ro09Amc&feature=emb_logo 4. Запишите примеры, разобранные в видеоуроке. 5. Выполните № 13.13(а) и №13.27(а) 6. Оцени себя и свою работу.
3.	Домашнее задание:	1. Выполните 3(базовый) и 4(профильный) вариант контрольно-измерительных материалов 2. Пришлите, выполненные задания 13.04.2020 на электронную почту

Приложение

12.

В таблице указаны средние цены (в рублях) на некоторые основные продукты питания в трех городах России (по данным на начало 2010 года).

Наименование продукта	Липецк	Ставрополь	Ярославль
Пшеничный хлеб (батон)
Молоко (1 литр)
Картофель (1 кг)
Сыр (1 кг)
Мясо (говядина) (1 кг)
Подсолнечное масло (1 литр)

Определите, в каком из этих городов окажется самым дешевым следующий набор продуктов: 3 л молока, 2 кг говядины, 1 л подсолнечного масла. В ответ запишите стоимость данного набора продуктов в этом городе (в рублях).

13.

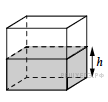
Вода в сосуде, имеющем форму правильной четырёхугольной призмы, находится на уровне h = 45 см. На каком уровне окажется вода, если её перелить в другой сосуд, имеющий форму правильной четырёхугольной призмы, у которого сторона основания втрое больше, чем у данного? Ответ дайте в сантиметрах.

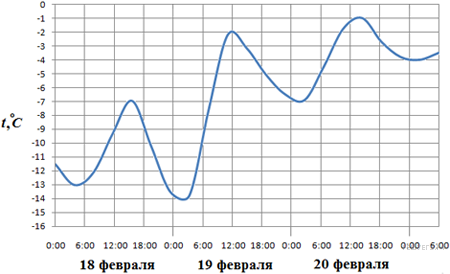
14.На рисунке показано изменение цены акций компании на момент закрытия биржевых торгов во все рабочие дни в период с 1 по 18 сентября 2006 года. По горизонтали указываются числа месяца, по вертикали — цена акции в рублях за штуку. Для наглядности точки соединены линией.

Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику изменения цены акций. В таблице под каждой буквой укажите соответствующий номер.

ПЕРИОДЫ ВРЕМЕНИ		ХАРАКТЕРИСТИКИ
А) 1−5 сентября Б) 6−8 сентября В) 11−13 сентября Г) 14−18 сентября		1) Наибольшее изменение цены за весь период. 2) Цена акций ежедневно снижалась 3) Цена акций ежедневно росла 4) Минимальное колебание цены акций

15. 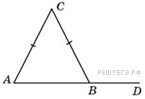В треугольнике . Внешний угол при вершине равен . Найдите угол 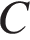. Ответ дайте в градусах.

16. Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 10. Найдите площадь боковой поверхности этой пирамиды.

17.На прямой отмечены точки A, B, C и D.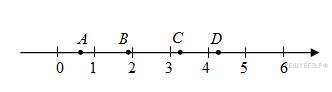

Каждой точке соответствует одно из чисел из правого столбца. Установите соответствие между указанными точками и числами.

ТОЧКИ		ЧИСЛА
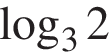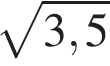A B C D		1) 2) 3) 4)

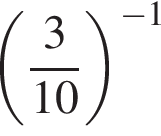
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

18.Некоторые сотрудники фирмы летом 2014 года отдыхали в Крыму, а некоторые — в Сочи. Все сотрудники, которые отдыхали в Сочи, не отдыхали в Крыму. Выберите утверждения, которые верны при указанных условиях.

1) Если сотрудник этой фирмы летом 2014 года отдыхал в Крыму, то он отдыхал и в Сочи.

2) Каждый сотрудник этой фирмы отдыхал летом 2014 года в Крыму.

3) Среди сотрудников этой фирмы, которые не отдыхали в Сочи летом 2014 года, есть хотя бы один, который отдыхал в Крыму.

4) Нет ни одного сотрудника этой фирмы, который летом 2014 года отдыхал и в Крыму, и в Сочи.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

19.Найдите четырёхзначное натуральное число, кратное 19, сумма цифр которого на 1 больше их произведения.

20.В корзине лежат 25 грибов: рыжики и грузди. Известно, что среди любых 11 грибов имеется хотя бы один рыжик, а среди любых 16 грибов хотя бы один груздь. Сколько рыжиков в корзине?

Вариант № 4

1.Для ремонта квартиры требуется 63 рулона обоев. Сколько пачек обойного клея нужно купить, если одна пачка клея рассчитана на 6 рулонов?

2.На рисунке жирными точками показан курс доллара, установленный Центробанком РФ, во все рабочие дни с 22 сентября по 22 октября 2010 года. По горизонтали указываются числа месяца, по вертикали — цена доллара в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьший курс доллара за указанный период. Ответ дайте в рублях.

3. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

4.Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 8 очков в двух играх. Если команда выигрывает, она получает 5 очков, в случае ничьей — 3 очка, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.

5.Решите уравнение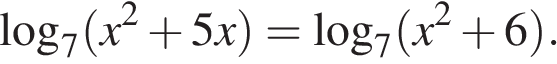

6. В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

7. 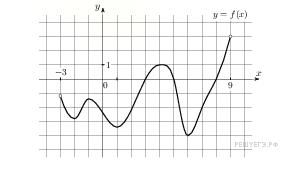На рисунке изображен график функции y = f(x), определенной на интервале (−3; 9) . Найдите количество точек, в которых производная функции f(x) равна 0.

8. Найдите объем многогранника, вершинами которого являются точки , , 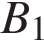, 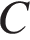правильной треугольной призмы 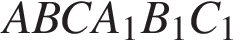, площадь основания которой равна 4, а боковое ребро равно 3.

Найдите значение выражения: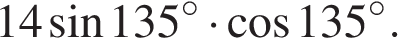

10.Перед отправкой тепловоз издал гудок с частотой Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону (Гц), где c — скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 3 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а 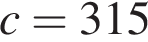м/с. Ответ выразите в м/с.

11.Из одной точки круговой трассы, длина которой равна 6 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 63 км/ч, и через 45 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

12.Найдите точку максимума функции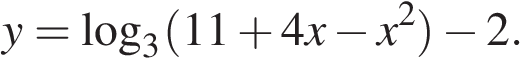

13.а) Решите уравнение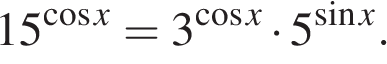

б) Найдите все корни этого уравнения, принадлежащие отрезку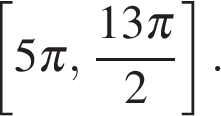

14.В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 8. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.

а) Докажите, что плоскость α делит медиану CE основания в отношении 5 : 1, считая от точки C.

б) Найдите объём пирамиды, вершиной которой является точка C, а основанием — сечение пирамиды SABC плоскостью α.

15.Решите неравенство: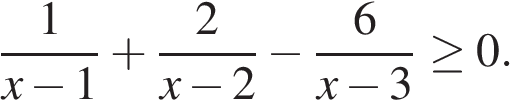

16.В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8, AC = 7.

а) Докажите, что вокруг этого четырёхугольника можно описать окружность.

б) Найдите BD.

17.Банк под определенный процент принял некоторую сумму. Через год четверть накопленной суммы была снята со счета. Банк увеличил процент годовых на 40 процентных пунктов (то есть увеличил ставку а% до (а + 40)%). К концу следующего года накопленная сумма в 1,44 раза превысила первоначальный вклад. Каков процент новых годовых?

18.Найдите все значение a, при каждом из которых уравнение

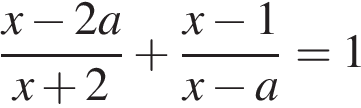
имеет ровно один корень.

19.Два игрока ходят по очереди. Перед началом игры у них есть поровну горошин. Ход состоит в передаче сопернику любого числа горошин. Не разрешается передавать такое количество горошин, которое до этого уже кто‐то в этой партии передавал. Ноль горошин тоже передавать нельзя. Тот, кто не может сделать очередной ход по правилам, — считается проигравшим. Начинающий или его соперник победит в этой игре, как бы ни играл партнёр?

Рассмотрите случаи:

а) у каждого по две горошины;

б) у каждого по три горошины;

в) у каждого по N горошин.