ОПРЕДЕЛИТЕЛИ И ИХ ВЫЧИСЛЕНИЕ. Определитель матрицы и его свойства

ОПРЕДЕЛИТЕЛИ И ИХ ВЫЧИСЛЕНИЕ

1. Определитель матрицы и его свойства.

2. Вычисление определителя методом Гаусса.

Определитель матрицы и его свойства

Каждой квадратной матрице по вполне определенному правилу может быть проставлено в соответствие число. Это число называется определителем⁴ или детерминантом.

Определение. Определительквадратной матрицы порядка 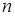- многочлен от элементов матрицы 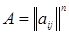, каждый член которого является произведением 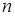элементов, взятых по одному из каждой строки и каждого столбца, и снабжен определенным знаком, т.е. многочлен вида

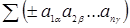В этой формуле суммирование производится по всем перестановкам 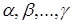чисел 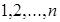и перед членом берется знак (+), если перестановка четна, и знак (-), если эта перестановка нечетна. Таким образом, определитель содержит 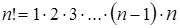членов, половина из которых берется со знаком «+», а другая – со знаком «-». Число 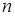называется порядком определителя. Подробнее – в [3].

_____________________

⁴Термин «определитель» в современном его значении ввел Огюстен Коши (1789-1857г.г.) в 1815 году. При решении систем линейных уравнений определители использовались немецким математиком Готфридом Лейбницем (1646 – 1716г.г.) и швейцарским математиком Габриэлем Крамером (1704 – 1752г.г.).

_____________________

Для определителя матрицы 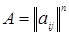приняты обозначения

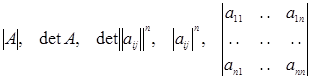Для 2-го и 3-го порядков формула принимает вид

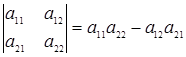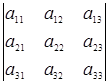
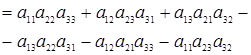При вычислении определителей 2-го и 3-го порядков можно пользоваться схемами

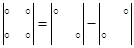
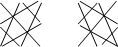
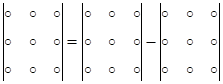
Для вычисления определителей более высоких порядков существуют специальные методы, некоторые из которых будут рассмотрены в дальнейшем.

Пример 2

Найти определитель матрицы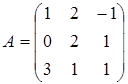

= .

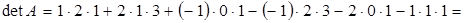
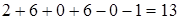Определители обладают рядом важных свойств, которые облегчают, в частности, их вычисление. Простейшие из этих свойств следующие.

1. Определитель не изменится при транспонировании матрицы, т.е. .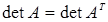

2. Если одна из строк (или столбец) определителя состоит из нулей, то он равен нулю.

3. Определитель изменит знак, если поменять местами любые две строки (или два столбца) матрицы.

4. Определитель равен нулю, если элементы двух строк (или столбца) матрицы соответственно пропорциональны.

5. Общий множитель всех элементов любой строки (или столбца) можно вынести за знак определителя.

6. Определитель не изменяется, если к элементам одной строки (столбца) прибавить элементы другой строки (столбца), умноженные на произвольный числовой множитель.

7. Определитель треугольной матрицы равен произведению элементов её главной диагонали.

8. Определитель произведения матриц равен произведению определителей матриц сомножителей.

Перечисленные свойства могут быть получены как следствия теоремы Лапласа, рассматриваемой в следующем разделе курса.

Вычисление определителя методом Гаусса⁵

Метод Гаусса основан на использовании свойств 3,6 и 7. Преобразуя определитель по свойствам 3 и 6, приводим его к треугольному виду, а затем вычисляем, пользуясь свойством 7.

______________________

⁵Карл Гаусс (1777 – 1855г.г.) – немецкий математик.

______________________

Пример 3

Вычислить методом Гаусса определитель .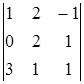

Сначала умножим первую строчку на –3 и добавим к третьей. Затем вторую строку умножим на и добавим к третьей.

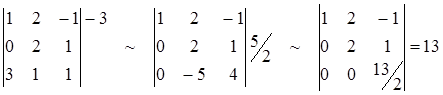Определение. Алгебраическое дополнение элемента квадратной

Матрицы 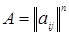есть число 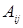, определяемое равенством ,

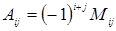где 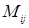– дополнительный минор элемента , равный определителю, получаемому из определителя матрицы 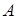вычеркиванием 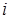-й строки и 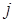-го столбца.

Теорема Лапласа. Если в квадратной матрице порядка 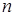выбрана произвольная строка (или столбец), то сумма произведений элементов этой строки (или столбца) на соответствующие алгебраические дополнения равна определителю этой матрицы.

Например, раскрывая определитель по элементам первой строки

или, раскрывая определитель по элементам первого столбца

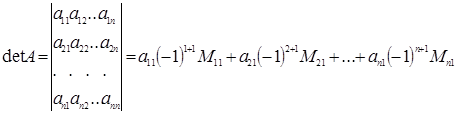получаем значение определителя через миноры, порядок которых на единицу меньше.

Теорема позволяет свести задачу вычисления определителя высокого порядка к вычислению определителей более низкого порядка. Так, в случае определителя 3-го порядка имеем

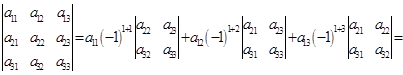
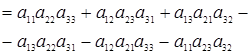что совпадает с полученным ранее выражением.