Хелпикс

Главная

Контакты

Случайная статья



Образовательный минимум. Модуль 10. Последовательности.. Примерная проверочная работа (зачёт).



Образовательный минимум

Модуль 10. Последовательности.

Сдать до10.02.2017

Критерии оценивания:

Учебный модуль «последовательности» состоит из двух частей: «основной» и «дополнительной» (всего 9 заданий). Для получения «зачёта» по модулю (оценка «3») необходимо написать в классе (в тетради для контрольных работ) проверочную работу, правильно решив не менее 5 заданий из «основной части» ( не менее четырёх заданий из «последовательности и арифметическая прогрессия» и одного задания из «геометрическая прогрессия».

Оценка «4» ставится за правильно выполненные 6 заданий из «основной» части и 1 задание из «дополнительной».

Оценка «5» ставится за правильно выполненные 7 заданий из «основной части и 1 задание из «дополнительной».

Все решения записываются полностью.

Задания для самоподготовки:

https://math-oge.sdamgia.ru/test?theme=48

https://math-oge.sdamgia.ru/test?theme=9

https://math-oge.sdamgia.ru/test?theme=47

Примерная проверочная работа (зачёт).

Основная часть

Последовательности и арифметическая прогрессия

1. Какими должны быть два следующих числа последовательности: 4, 10, 5, 12, 6, 14,...

2. По­сле­до­ва­тель­ность за­да­на фор­му­лой 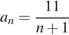. Сколь­ко чле­нов в этой по­сле­до­ва­тель­но­сти боль­ше 1?

   1) 8 2) 9  3) 10 4) 11

3. В ариф­ме­ти­че­ской про­грес­сии 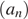из­вест­но, что 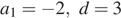. Най­ди­те четвёртый член этой про­грес­сии.

4. Дана ариф­ме­ти­че­ская про­грес­сия (an), раз­ность ко­то­рой равна −2,5, a1 = −9,1. Най­ди­те сумму пер­вых 15 её чле­нов.

5. Ариф­ме­ти­че­ская про­грес­сия за­да­на усло­ви­я­ми: 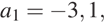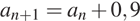. Най­ди­те сумму пер­вых 19 её чле­нов.

Геометрическая прогрессия

6. В гео­мет­ри­че­ской про­грес­сии 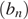из­вест­но, что 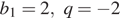. Найти пятый член этой про­грес­сии.

7. Гео­мет­ри­че­ская про­грес­сия за­да­на усло­ви­ем b1 = −7, bn + 1 = 3bn. Най­ди­те сумму пер­вых 5 её чле­нов.

Дополнительная часть

8*. В пер­вом ряду ки­но­за­ла 24 мест, а в каж­дом сле­ду­ю­щем на 2 места боль­ше, чем в преды­ду­щем.. Сколь­ко мест в Сколько мест в ряду с но­ме­ром ? Ва­ри­ан­ты от­ве­та:
1.   2.   3.   4.  

 

9*. Гео­мет­ри­че­ская про­грес­сия за­да­на усло­ви­ем 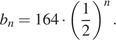Най­ди­те сумму пер­вых её 4 чле­нов.
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.