
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольная работа. Задание на расчет
Белорусский национальный технический университет
Кафедра "Электротехника и электроника"
Контрольная работа
по дисциплине " Электротехника"
Тема: Методы расчёта электрических цепей постоянного тока
Исполнитель:
студент группы 30802113
________________________
Руководитель: преподаватель кафедры
"Электротехника и электроника"
В.Д. Ежов
Минск 2015
Задание на расчет
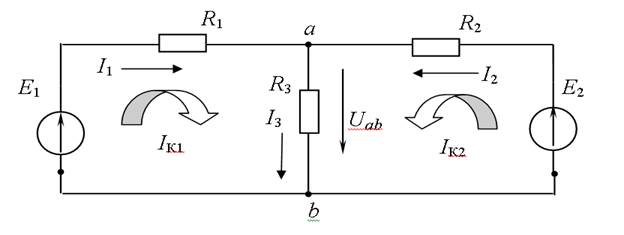
Рис. 1 Расчетная схема
| ВАРИАНТ ЗАДАНИя | R1, Ом | |
| R2, Ом | ||
| R3, Ом | ||
| Е1, B | ||
| Е2, B |
1.Метод двух узлов
Применяется для расчета цепей, имеющих только два узла.
1.1. Напряжение между узлами a и b
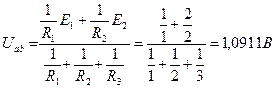 ;
;
1.2. Ток ветви 1
I1 = (E1– Uab)/R1 = (1 – 1.0911)/1 = –0.0911 A
1.3. Ток ветви 2
I2 = (E2– Uab)/R2 = (2 – 1.0911)/2 = 0.4545 A
1.3. Ток ветви 3
I3 = Uab/R3 = (2 – 1.0911)/3 = 0.3636 A
Проверка I1 + I2 – I3 = –0.091 + 0.4545 – 0.3636 = – 0,0002 А
2.Метод контурных токов
2.1. Цепь разбивают на отдельные контуры и в каждом контуре произвольно выбирают направление условно действующего контурного тока, замыкающегося только в данном контуре;
2.2. Выбрав обход контуров, совпадающим с направлением контурных токов, для каждого контура записывают уравнение по второму закону Кирхгофа в матричной форме. При этом учитывают падения напряжения на элементах рассматриваемого контура и от соседних контурных токов;
| E1 | = | (R1 + R3) | R3 | x | Ik1 |
| E2 | R3 | (R2 + R3) | Ik2 |
2.3. Вычисляем определитель
| Δ = | (R1 + R3) | R3 |
| R3 | (R2 + R3) |
= (R1 + R3) · (R2 + R3) – R3 · R3 =
= (1 + 3) · (2 + 3) – 32 = 11 Ом2
2.4. Вычисляем миноры
| Δ1 = | E1 | R3 |
| E2 | (R2 + R3) |
= E1 · (R2 + R3) – E2 · R3 =
= 1 · (2 + 3) – 2 · 3 = – 1 Ом В
| Δ2 = | (R1 + R3) | E1 |
| R3 | E2 |
= (R1 + R3) · E2 – R3 · E1 =
= (1 + 3) · 2 – 3 · 1 = 5 Ом В
2.5. Определяем контурные токи
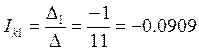 А
А
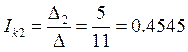 А
А
2.6. Действительные токи ветвей определяются алгебраическим суммированием контурных токов, протекающих в них. Определяем токи в ветвях (Рис.1)
I1 = Ik1 = – 0,0909 А
I2 = Ik2 = 0,4545 А
I3 = Ik1 + Ik2 = – 0,0909 + 0,4545 = 0,3636 А
3.Метод уравнений Кирхгофа
Порядок расчета:
– произвольно намечают направления токов ветвей;
– произвольно намечают направления обхода контуров и по второму закону Кирхгофа записывают уравнения. При этом контуры выбирают так, чтобы каждый из них содержал хотя бы одну, не учтенную ранее, ветвь;
– решая систему уравнений, находят токи. Если значения некоторых токов отрицательные, то действительные направления их будут противоположны первоначально выбранным .
3.1. Для электрической цепи рис. 1, расчет токов цепи осуществляется путем решения следующей системы уравнений:
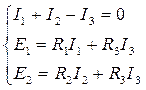 (1)
(1)
3.2. Делаем замену тока I3 в уравнениях
I3 = I1 + I2 (2)
E1 = R1I1 + R3I1+ R3I2 (3)
E2 = R2I2 + R3I1+ R3I2 (4)
3.3. Из (3) выражаем I1 через I2 и подставляем в (4)
I1 = (E1 – R3I2)/( R1 + R3) (5)
E2 = R2I2 + R3 (E1 – R3I2)/( R1 + R3) + R3I2 (6)
3.4. Из (6) находим значение тока I2
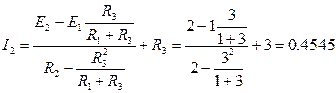 A
A
3.5. Из (5) находим значение тока I1
I1 = (E1 – R3I2)/( R1 + R3) = (1 – 3·0.4545)/(1+3) = –0.0909 A
3.6. Из (2) находим значение тока I3
I3 = I1 + I2 = –0.0909 + 0.4545 = 0.3636 A
3.7. Результаты расчета сводим в Таблицу 1
Таблица 1
| Е1, В | Е2, В | Uab, B | I1, A | I2, A | I3, A | Метод расчета |
| 1.0911 | –0.0909 | 0.4545 | 0.3636 | Метод двух узлов | ||
| – | –0.0909 | 0.4545 | 0.3636 | Метод контурных токов | ||
| – | –0.0909 | 0.4545 | 0.3636 | Законы Кирхгофа |
4.Метод наложения
Основан на принципе наложения, согласно которому в линейной электрической цепи, содержащей несколько источников питания, токи ветвей рассматривают как алгебраическую сумму токов, вызываемых в этих ветвях действием каждой ЭДС в отдельности.
Последовательность расчета:
4.1. Оставляем в цепи источник E1 (Рис.2)
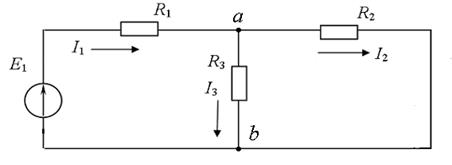 Рис.2
Рис.2
4.2. Ток I1(1) от э.д.с. E1 после свертки сопротивлений R2 и R3
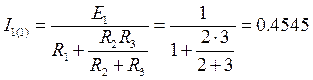 А
А
4.3. Напряжение Uab(1) от э.д.с. E1
Uab(1) = E1 – R1 I1(1) = 1 – 1· 0,4545 = 0,5454 В
4.4. Токи I2(1) и I3(1) от э.д.с. E1
I2(1) = Uab(1)/ R2 = 0,5454/2 = 0,2727 А
I3(1) = Uab(1)/ R3 = 0,5454/3 = 0,1818 А
4.5. Оставляем в цепи источник E2 (Рис.3)
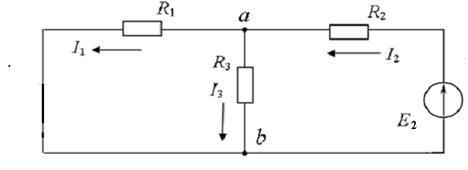 Рис.3
Рис.3
4.6. Ток I2(2) от э.д.с. E2 после свертки сопротивлений R1 и R3
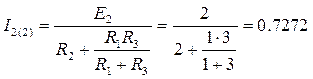 А
А
4.7. Напряжение Uab(2) от э.д.с. E2
Uab(2) = E2 – R2 I2(2) = 2 – 2· 0,7272 = 0,5454 В
4.8. Токи I1(2) и I3(2) от э.д.с. E2
I1(2) = Uab(2)/ R1 = 0,5454/1 = 0,5454 А
I3(2) = Uab(2)/ R3 = 0,5454/3 = 0,1818 А
4.9. Действительные токи ветвей находим суммированием (наложением) соответствующих токов расчетных схем с учетом их направлений. Результаты расчета сводим в Таблицу 2
Таблица 2
| Е1, В | Е2, В | I1, A | I2, A | I3, A | |
| Частичные токи от ЭДС Е1 | 0,4545 | –0,2727 | 0,1818 | ||
| Частичные токи от ЭДС Е2 | –0,5454 | 0,7272 | 0,1818 | ||
| Действительные токи (Σ) | –0,0909 | 0,4545 | 0,3636 |
5. Мощности источников и приемников энергии
5.1. Мощности источников Е1 и Е2
P1 = Е1 I1 = 1· (–0,0909) = –0,0909 Вт (Источник потребляет энергию)
P2 = Е2 I2 = 2· 0,4545= 0,909 Вт (Источник вырабатывает энергию)
5.2. Мощности потребителей R1, R2 и R3
p1 = I12· R1 = (–0,0909)2·1 = 0,00826 Вт
p2 = I22· R2 = 0,45452·2 = 0,4131 Вт
p3 = I32· R3 = 0,36362·3 = 0,3966 Вт
5.3. Баланс мощностей потребителей R1, R2 и R3
ΣP = P1 + P2 = –0,0909 + 0,909 = 0.8181 Вт
Σp = p1 + p2 + p3= 0,00826 + 0,4131 + 0,3966 = 0,81796 Вт
ΣP ≈ Σp
7. Используемая литература
7.1. Евдокимов Ф. Е. Теоретические основы электротехники. - М., 1981.
7.2. Попов В. С. Теоретическая электротехника. - М., 1990.
7.3. Касаткин А. С., Немцов М. В. Электротехника. - М., 2000.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|