Хелпикс

Главная

Контакты

Случайная статья



Математикалық маятниктің тербелісін үйрену

Стр 1 из 2Следующая ⇒


1. Математикалық маятниктің тербелісін үйрену

Жұмыстың мақсаты: Математикалық маятник тербелісі периодының маятниктің ұзындығына, амплитудасына және массасына тәуелділігін эксперимент арқылы тексеру.

Құрал-жабдықтар:Штатив, жібі бар шар, таразы, өлшеуіш сызғыш, транспортир, пластилин, магнит.       Зертханалық тұрғы және муфта, секундомер, өлшеуіш таспа.

Теориялық түсінік:

Математикалық маятник тербеліс периодының формуласын қорытып шығарайық .

Есепті жеңілдету үшін маятникті бір жазықтықта тербелтпей, жүк шеңбер бойымен қозғалатындай етіп, оны конус сызуға мәжбүр етеміз.

Маятниктің айналу периоды оның тербеліс периодына тең болады. Тайн.=Ттер=Т.

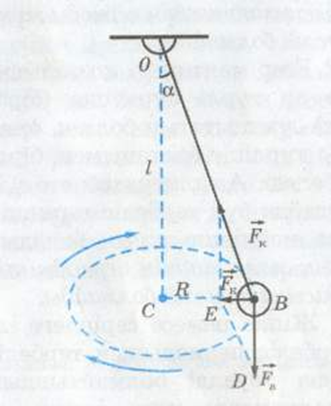Конустық маятниктің айналу  периоды жүк сызатын шеңбердің ұзындығын сызықтық жылдамдыққа бөлгенге тең:

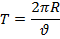
Ал маятник вертикаль күйінен шамалы ғана ауытқитын болса, амплитуда аз болғанда, қорытқы күш шеңбердің ВС радиусы бойымен бағытталады деп есептеуге болады. Бұл жағдайда қорытқы күш центрге тартқыш күшке тең:

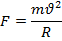
ОВС және ВDE үшбұрыштарының ұқсастығынан: ВЕ:ВD = СВ:ОС немесе Ғ:mg = R:l, бұдан    

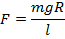
Ғ күшінің осы екі өрнегін теңестіре отырып алатынымыз:

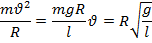
Осыны Т периодтың өрнегіне қойып, мынаны аламыз:

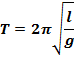
Гипотеза:

· Математикалық маятниктің периоды маятник ұзындығына тәуелді болуы мүмкін.

· Математикалық маятниктің периоды жүктің массасына тәуелді емес болуы мүмкін.

· Математикалық маятниктің периоды тербеліс амплитудасына тәуелді емес болуы мүмкін.

· Математикалық маятниктің периоды еркін түсу үдеуіне тәуелді болуы мүмкін.

Аспаптың бөлік құны және аспаптық қателік:

Аспап шкаласындағы бөліктің құны өлшенетін шаманың шкаладағы кез келген екі мәнінің айырымын сол мәндердің арасындағы бөліктердің санына бөлу арқылы анықталады.

Аспаптық қателік аспап бөлігі құнының жартысына тең.


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.