Хелпикс

Главная

Контакты

Случайная статья



К.Р. ВЕКТОРНАЯ АЛГЕБРА. Вариант 1. Вариант 2



К.Р. ВЕКТОРНАЯ АЛГЕБРА

Вариант 1

1. Вектор 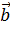  составляет с координатными осями  OY  и  OZ  углы b = 60° и g = 60°. Вычислить его координаты, если .

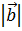2. Найти вектор 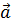, коллинеарный вектору  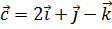и удовлетворяющий условию .

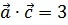3. Найти длину вектора 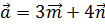, если .

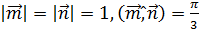4. Даны векторы 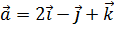, 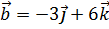. Найти проекцию вектора  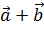на вектор .

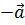5. Дан треугольник с вершинами А(-2, 3, 1), В(-2, -1, 4), С(-2, -4, 0). Определить его внешний угол при вершине С.

6. Найти вектор 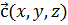, перпендикулярный к векторам  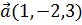и .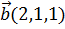

7. Найти высоту АК треугольника АВС с вершинами А(-3, -2, -4), В(-1, -4, -7), С(1, -2, 2).

8. Даны три силы 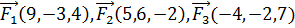, приложенные к точке С(-5, 4, -2). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку В(4, 6, -5).

9. Вычислить объем пирамиды с вершинами в точках А(-4, -4, -3), В(-2, -1,1), С(2, -2, -1), D(-1, 3, -2) и высоту СК, опущенную из вершины С на АВD.

10.  При каком значении λ векторы 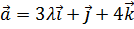, , 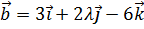 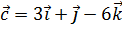будут компланарны?

 

 

Вариант 2

 

1. Вектор , коллинеарный вектору 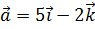 j,образует острый угол с осью OZ. Найти координаты вектора , если .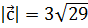

2. Радиус-вектор 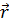 точки М(x, y, z) составляет с осью ОУ угол 60°, а с осью ОZ угол 45°, его длина 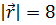. Найти координаты точки М, если ее абсцисса отрицательна.

3. При каких значениях α и β вектор 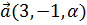 перпендикулярен вектору 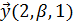, если ?

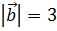4. Даны вершины треугольника А(-1, -2, 4), В(-4, -2,0), С(3, -2, 1). Определить его внутренний угол при вершине В.

5. Даны три вектора 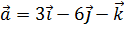, , 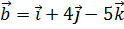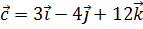. Вычислить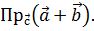

6. В треугольнике с вершинами А(1, -1, 2), В(5, -6,2) и С(1, 3, -1) найти высоту ВD.

7. Найти координаты вектора 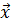, если известно, что он перпендикулярен векторам  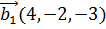и 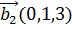, образует с ортом  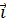тупой угол и .

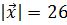8. Даны три силы 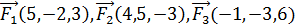, приложенные к точке К(7, 1, -5). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку N(2, -3, -6).

9. Даны вершины пирамиды А(0, 6, 4), В(3, 5,3), С(-2, 11, -5), D(1, -1, 4). Найти ее объем и длину высоты, проведенной из вершины А к грани ВСD.

10. При каком значении λ точки А(1, 2, λ), В(0, 1,5), С(-1, -2, -1), D(2, 1, λ) лежат в одной плоскости?

 

 

Вариант 3

1. Даны две координаты вектора: x = 2, y = - 3. Определить его третью координату z и направляющие косинусы, если его модуль равен 7.

2. Вектор 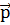, коллинеарный вектору  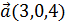образует с осью ОХ тупой угол. Найти координаты вектора 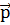, зная, что .

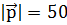3. Найти такое число a, чтобы косинус угла между векторам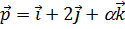и  и 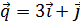 был равен .

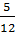4. Даны три вектора 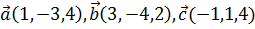. Вычислить проекцию вектора  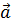на вектор .

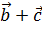5. Найти вектор 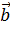, ортогональный векторам  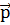и 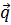 и удовлетворяющий условию 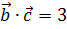, если .

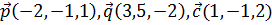6. Найти длину высоты СК треугольника АВС с вершинами А(2, 2, 2), В(4, 0, 3), С(1, 1, 0).

7. На векторах 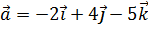 и 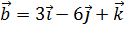 построен параллелограмм. Найти его высоту, опущенную из конца вектора .

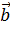8. Даны три силы 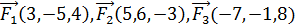, приложенные к точке С(-3, 5, 9). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку В(5, 6, -3).

9. Дана пирамида с вершинами в точках А(1, 2, 3), В(-2, 4, 1), С(7, 6, 3) и D(4, -3, 1). Найти ее объем и длину высоты, проведенной из вершины А на грань ВСD.

10.  При каком значении y точка М(2, y, 0) будет лежать в плоскости точек А(3, -4, 1), В(2, 5, 0), С(-1, 3, 2)?

 

 

Вариант 4

1. Известны модуль вектора 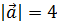 и два угла, образуемые им с координатными осями: a = 60°, b = 120°. Найти координаты вектора .

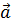2. Найти координаты вектора 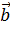, коллинеарного вектору  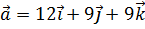при условии, что вектор  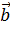образует с осью ОХ тупой угол и его модуль равен .

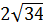3. Даны вершины треугольника А(3, 2, -3), В(5, 1, -1), С(1, -2, 1). Определить его внешний угол при вершине А.

4. Даны векторы 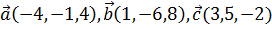. Найти проекцию вектора  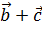на вектор .

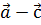5. Найти единичные векторы 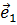 и 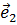, ортогональные векторам  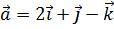и .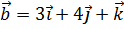

6. Треугольник построен по векторам 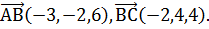 Вычислить длину высоты AD.

7. Вычислить высоты параллелограмма, построенного на векторах , .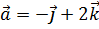

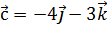8. Три силы 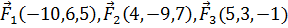 приложены к точке Е(4, -5, 9). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку N(4, 7, -5).

9. Вершины пирамиды находятся в точках А(-4, -2, -3), В(2, 5, 7), С(6, 3, -1), D(6, -4, 1). Найти объем пирамиды и высоту, опущенную на грань ACD.

10.  Даны векторы 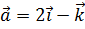, , 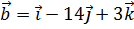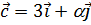. Определить значение a, при котором вектор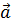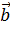ы , ,  компланарны.

 

Вариант 5

1. Известны модуль вектора 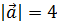 и два угла, образуемые им с координатными осями: a = 60°, g = 120°. Найти координаты вектора .

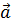2. Вектор 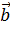 коллинеарен вектору 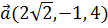, образует с осью ОУ острый угол и имеет длину, равную 10. Найти его координаты.

3. Даны два вектора: 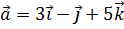, 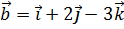. Найти вектор  при условии, что он перпендикулярен оси OZ и удовлетворяет условиям , .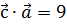

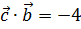4. Даны три вектора: 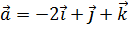,  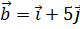и 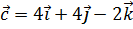. Вычислить .

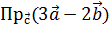5. Найти координаты вектора 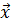, если известно, что он перпендикулярен векторам  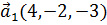и 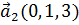, образует с ортом  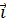тупой угол и .

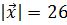6. Дан треугольник с вершинами А(2, 2, 2), В(0, 1, 0), С(4, 0, 3). Найти его площадь и высоту ВD.

7. Найти единичный вектор, ортогональный векторам 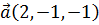 и .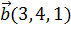

8. Даны три силы 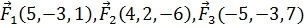, приложенные к точке В(-5, 3, 7). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку К(3, 8, -5).

9. Вершины   пирамиды   находятся в точках  А(4, 2, 3),  В(-5, -4, 2),   С(5, 7, -4), D(6, 4, -7). Найти объем пирамиды и высоту, опущенную на грань AВD.

10.  Даны векторы 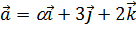, , 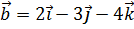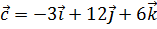. При каком значении a эти векторы компланарны?

 

Вариант 6

1. Вектор 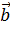, параллельный плоскости XOY, образует с осью ОХ угол 45°, а с осью OY – тупой угол. Известно, что 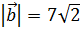. Найти координаты вектора .

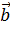2. Вектор 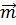 коллинеарен вектору  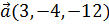и образует с осью OY острый угол. Найти координаты вектора 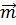, если .

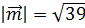3. Даны вершины треугольника АВС: А(-1, -2, 4), В(-4, -2, 0), С(3,-2, 1). Вычислить внешний угол при вершине В.

4. При каком значении a векторы 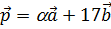 и 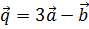 ортогональны, если , , ?

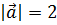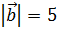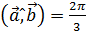5. Вектор 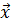 перпендикулярен векторам ,  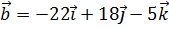и образует с осью ОХ тупой угол. Найти его координаты, если .

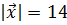6. Дан треугольник с вершинами А(-4, -2, -5), В(0, -7, -2), С(0, -2, -7). Вычислить длину его высоты ВD.

7. Определить y из условия, что площадь параллелограмма, построенного на векторах 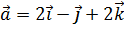,  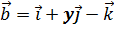равна .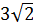

8. Даны три силы 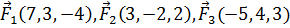, приложенные к точке L(-5, 0, 4). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку К(4, -3, 5).

9. Вершины пирамиды находятся в точках А(3,5,3), В(-3,2,8), С(-3, -2, 6), D(7, 8, -2). Найти объем пирамиды и высоту, опущенную на грань ACD.

10. Определить, при каком значении x точка М(x, 0, 0) будет лежать в плоскости точек А(6, 2, 1), В(3, -1, 2), С(2, 0, 1).

 

 

Вариант 7

1. Вектор , параллельный плоскости YOZ, составляет с осью OY угол 135°. Найти координаты вектора , если .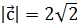

2. Вектор 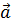 коллинеарен вектору 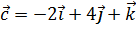. Найти координаты вектора 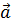, если он удовлетворяет условию 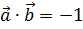, где .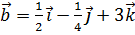

3. Даны векторы 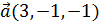 и 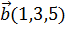.Найти проекцию вектора  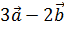на вектор .

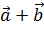4. Даны вершины треугольника: А(-2, 3, 1), В(4, 0, -3), С(1, -5, -1). Определить косинус угла между медианами ВМ и AN треугольника АВС.

5. Вектор 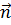, перпендикулярный векторам  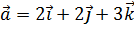и 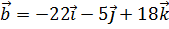, образует с осью OZ тупой угол. Найти его координаты, зная, что .

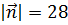6. Найти длину высоты AD треугольника АВС, если , .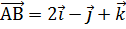

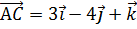7. Найти единичные векторы 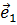 и 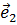, перпендикулярные векторам  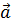и 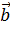, если , .

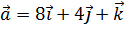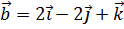8. Даны три силы 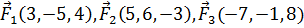, приложенные к точке D(-3, 5, 9). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку Q(5, 6, -3).

9. Дана пирамида с вершинами в точках А(- 9, -7, 4), В(- 4, 3, -1), С(5, -4, 2), D(3, 4, 4). Найти ее объем и длину высоты, опущенной на грань BCD.

10.  Определить, при каком значении l векторы 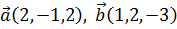,  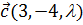компланарны.

 

 

Вариант 8

1. Радиус-вектор точки М составляет с осью ОХ угол 120°, а с осью ОZ угол 135°; его длина равна 10. Найти координаты точки М, если ее ордината отрицательна.

2. Вектор 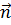, коллинеарный вектору 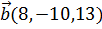, образует с осью ОZ тупой угол. Зная, что 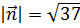, найти его координаты.

3. Даны векторы 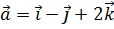, 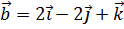. Найти проекцию вектора  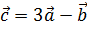на направление вектора .

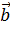4. Даны вершины треугольника АВС: А(2, -3, 0), В(-1, -4, 1), С(5, 2, 3). Найти косинус угла между медианами АМ и СN.

5. Даны векторы 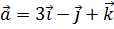, 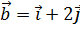. Найти a и b, при которых вектор  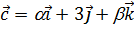коллинеарен вектору .

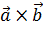6. Даны точки А(1, 2, 0), В(3, 0, -3), С(5, 2, 6). Вычислить площадь треугольника АВС и его высоту CD.

7. Найти вектор 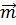, ортогональный векторам  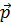и 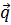 и удовлетворяющий условию 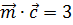, если .

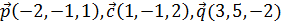8. Даны три силы 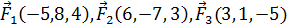, приложенные к точке A(2, -4, 7). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку B(0, 7, 4).

9. Дана пирамида с вершинами в точках А(4, 3, 1), В(2, 7, 5), С(-4,-2, 4), D(2, -3, -5). Найти ее объем и длину высоты, проведенной к грани АCD.

10.  При каком значении λ векторы 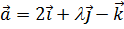, , 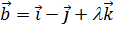 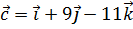будут компланарны?

 

 

Вариант 9

1. Вектор 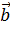 коллинеарен вектору  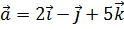и удовлетворяет условию 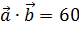. Найти координаты вектора .

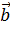2. Вектор 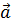 составляет с осями координат острые углы α,  β,  γ, причем α = 45°,β = 60°. Найти его координаты, если .

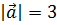3. Даны векторы 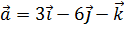,  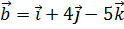и 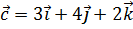. Найти проекцию вектора  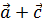на вектор .

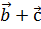4. Даны вершины четырехугольника А(1, -2, 2), В(1, 4, 0), С(-4, 1, 1), D(-5, -5, 3). Вычислить угол φ между его диагоналями.

5. Вектор 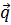, перпендикулярный векторам  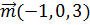и 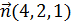, образует с оcью OZ тупой угол. Найти его координаты, если .

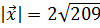6. В треугольнике с вершинами А(1, 3, 1), В(-2, -3, 4), С(3, 4, -4) найти высоту AD.

7. Найти единичный вектор, ортогональный векторам 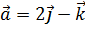 и 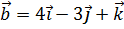 и образующий с ортом  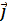острый угол.

8. Даны три силы 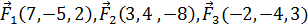, приложенные к точке С(-3, 2, 0). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку D(6, 4, -3).

9. Вершины пирамиды находятся в точках А(2, 3, 4), В(4, 7, 3), С(1, 2, 2) и D(-2, 0, -1). Вычислить объем пирамиды и длину ее высоты, опущенной из вершины А на грань BCD.

10.  Определить, при каком значении λ векторы 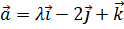, , 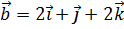 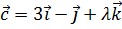будут компланарны.

 

 

Вариант 10

1. Вектор , лежащий в плоскости ХOY, образует с осью OХ  угол a = 120°, а с осью ОY – тупой угол b. Найти координаты вектора , если .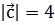

2. Дан вектор 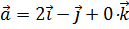. Найти вектор , коллинеарный вектору 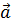, если .

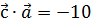3. Определить, при каком значении l векторы 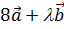 и 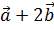 будут взаимно перпендикулярны, если , , .

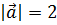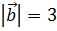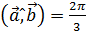4. Даны векторы 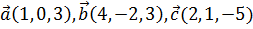. Найти проекцию вектора  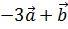на вектор .

5. В треугольнике АВС с вершинами в точках А(1, 1, -1), В(2, 3, 1), С(3, 2, 1) найти острый угол между медианой ВD и стороной АС.

6. Найти единичный вектор 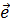, перпендикулярный векторам  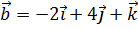и 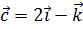 и образующий с ортом  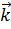острый угол.

7. Вычислить площадь треугольника с вершинами В(-2, 5, -3), С(3, -2, 4), D(1, 2, 2) и найти его высоту BF.

8. Даны силы 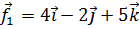 и 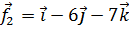. Найти работу их равнодействующей при перемещении точки приложения сил из начала координат в положение М(-3, -4, 1).

9. Вершины пирамиды находятся в точках А(-8, 2, 7), В(3, -5, 9), С(2, 4, -6), D(4, 6, -5). Найти объем пирамиды и высоту, опущенную на грань АCD.

10.  Доказать, что точки А(1, 2, -1), В(0, 1, 5), С(-1, 2, 1) и D(2, 1, 3) лежат в одной плоскости.

 

Вариант 11

1. Вектор 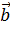, лежащий в плоскости ХOZ, образует с осью OZ  угол g = 150°, а с осью ОX – тупой угол. Найти координаты вектора 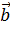, если его длина равна .

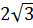2. Найти вектор 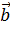, коллинеарный вектору  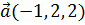и удовлетворяющий условию .

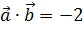3. Найти длину вектора 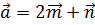, если , , .

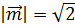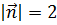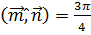4. Даны вершины треугольника А(-1, -2, 4), В(-4, -2, 0) и С(3,-2,1). Найти его внутренний угол при вершине А.

5. Найти проекцию вектора 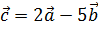 на вектор 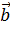, если , .

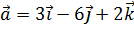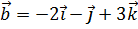6. Найти единичный вектор, ортогональный векторам 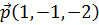 и 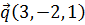 и образующий с ортом  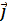острый угол.

7. Найти длину высоты ВК треугольника ВСD, если , .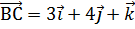

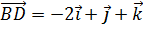8. Даны три силы: 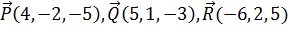, приложенные к точке В(-3, 2, -6). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку С(4, 5, -3).

9. Дана пирамида с вершинами в точках А(7, 4, 2), В(-5, 3, -9), С(1,-5, 3), D(7, -9, 1). Найти ее объем и длину высоты, опущенной из вершины С на грань АВD.

10. Установить, компланарны ли векторы .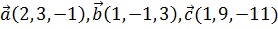

 

Вариант 12

1. Вектор 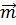, лежащий в плоскости YOZ, образует с осью OZ  угол g = 150°, а с осью ОY – острый угол b. Найти координаты вектора 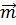, если .

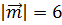2. Вектор 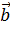 коллинеарен вектору  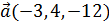и имеет противоположное с ним направление. Найти координаты вектора 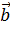, если .

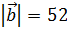3. Даны векторы 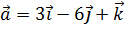,  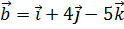и 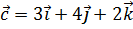. Найти проекцию вектора  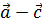на вектор .

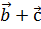4. Дан треугольник с вершинами А(-2, 3, 1), В(-2, -1, 4), С(-2, -4, 0). Определить его внутренний угол при вершине С.

5. Вектор 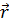 ортогонален векторам 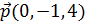,  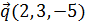и удовлетворяет условию 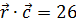. Найти координаты вектора 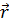, если .

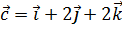6. Дан треугольник с вершинами в точках А(4, 2, 5), В(0, 7, 2), С(0, 2, 7). Вычислить длину высоты ВD.

7. Вектор 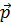, перпендикулярный векторам 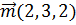, , 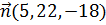образует с осью OY тупой угол. Найти координаты вектора 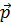, если .

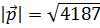8. Вычислить работу силы 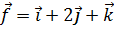 при перемещении материальной точки из положения М1(-1, 2, 0) в положение М2(2, 1, 3).

9. Вершины пирамиды находятся в точках А(-6, -3, -5), В(5, 1, 7), С(3, 5, -1), D(4, -2, 9). Найти ее объем и длину высоты, опущенной из вершины В на грань АCD.

10. Установить, компланарны ли векторы , , .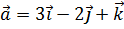

 

 

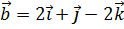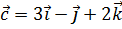Вариант 13

1. Вектор 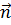, параллельный плоскости XOY, образует с осью OY угол b = 45°, а с осью OX – тупой угол a. Найти его координаты, если .

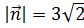2. Вектор 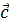 коллинеарен вектору  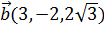и образует с осью OX тупой угол. Найти координаты вектора 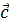, если .

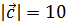3. Даны векторы 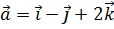, 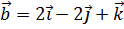. Найти проекцию вектора  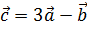на направление вектора .

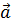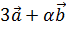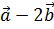4. Определить, при каком значении α векторы  и  будут взаимно перпендикулярны, есл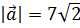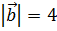и ,  и .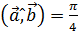

5. Найти острый угол между диагоналями параллелограмма, построенного на векторах 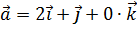 и .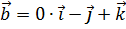

6. Вектор 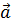 перпендикулярен векторам  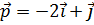и 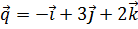 и имеет длину, равную 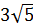. Найти координаты вектора .

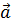7. Даны вершины треугольника А(1, −1, 2), В(5, −6, 2), С(1, 3, −1). Вычислить длину его высоты, опущенной из вершины В на сторону АС.

8. Даны силы 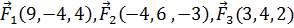, приложенные к точке N(5, −4, 3). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку K(4, −5, 9).

9. Вершины пирамиды находятся в точках А(3, 5, 4), В(8, 7, 4), С(5, 10, 4), D(4, 7, 8). Найти ее объем и длину высоты СЕ, опущенной на грань АВD.

10. Установить, компланарны ли векторы , , .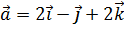

 

 

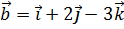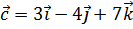Вариант 14

1. Вектор 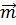, параллельный плоскости XOZ, образует с осью OZ угол γ = 30°, а с осью OX – острый угол a. Найти его координаты, если .

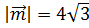2. Дан вектор 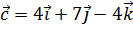. Найти вектор 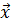, коллинеарный вектору  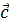и противоположного с ним направления, если .

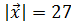3. Даны три вектора: 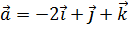,  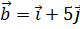и 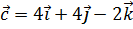. Вычислить .

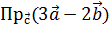4. Найти длину вектора 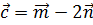, если , , .

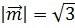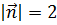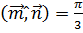5. Даны вершины треугольника: А(3, 2, -3), В(5, 1, -1), С(1, -2, 1). Найти внутренний угол при вершине А.

6. Найти единичный вектор, ортогональный векторам 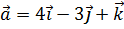 и 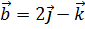 и образующий с ортом  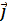тупой угол.

7. Найти площадь параллелограмма, построенного на векторах 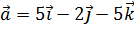,  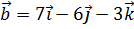и длины его высот.

8. Даны три силы 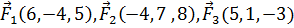, приложенные к точке В(-5, −4, 2). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку С(7, −3, 5).

9. Вершины пирамиды находятся в точках А(-2, -5, -1), В(-6, -7, 9), С(4, -5, 1), D(2, 1, 4). Найти ее объем и высоту, опущенную на грань ВСD.

10. Лежат ли точки А(1, 2, -1), В(4, 1, 5), С(-1, 2, 1), D(2, 1, 3) в одной плоскости?

 

Вариант 15

1. Радиус-вектор 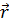 точки М составляет с осью ОY угол 60°, а с осью ОZ угол 45°; его длина 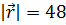. Найти координаты точки М, если ее абсцисса отрицательна.

2. Найти вектор 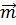, коллинеарный вектору  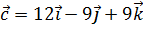и противоположного с ним направления, если .

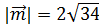3. Даны векторы 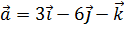,  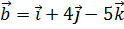и 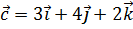. Найти проекцию вектора  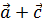на вектор .

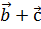4. Дан треугольник с вершинами А(2, −1, 6), В(3, 0, 5), С(5, 2, 6) найти угол между медианой АМ и стороной АВ.

5. Вектор 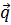 перпендикулярен векторам 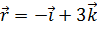,  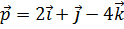и удовлетворяет условию 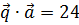. Найти координаты вектора 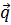, если .

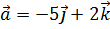6. На векторах 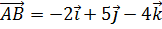 и 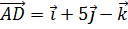 построен параллелограмм. Найти его площадь и высоту АК, опущенную на сторону ВС.

7. С помощью векторного произведения вычислить синус угла, образованного векторам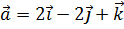и  и .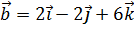

8. Даны три силы 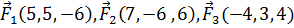, приложенные к точке Е(-9, 4, 7). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку L(8, −1, 7).

9. Вершины пирамиды находятся в точках А1(4, 2, 3), А2(-5, -4, 2), А3(5, 7, -4), А4(6, 4, -7). Вычислить ее объем и длину высоты, опущенной на грань А1А2 А3.

10. При каком значении λ векторы 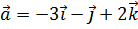, , 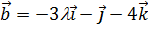 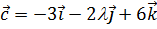будут компланарны?

 

 

Вариант 16

1. Вектор 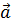, перпендикулярный оси OY, образует с осью ОХ угол 60°, а с осью OZ – тупой угол. Найти координаты вектора 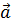, если .

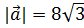2. Вектор 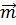 коллинеарен вектору  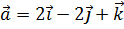и образует тупой угол с осью OZ. Зная, что 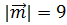, найти его координаты.

3. Даны векторы 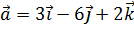 и 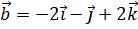. Найти проекцию вектора  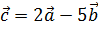на вектор .

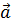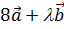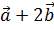4. Определить, при каком l векторы  и  будут взаимно перпендикулярны, есл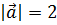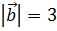и ,  и .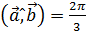

5. Даны четыре точки: А(1, 3, -1), В(2, 0, 3), С(4, -1, 5), D(3, 2, 1). Убедившись в том, что они являются вершинами параллелограмма, найти косинус угла между большей диагональю и стороной AD.

6. Найти единичный вектор 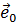, перпендикулярный векторам  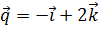и 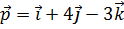 и образующий с ортом  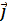острый угол.

7. Дан треугольник с вершинами В(7, 3, -1), С(6, -2, 0), D(3, 2, -7). Найти его площадь и длину высоты СМ.

8. Даны три силы 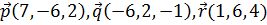, приложенные к точке С(3, -6, 1). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку D(6, -2, 7).

9. Вычислить объем пирамиды с вершинами в точках А(2, -3, 5), В(0, 2, 1), С(-2, -2, 3), D(3, 2, 4) и длину ее высоты, опущенной на BCD.

10. Даны векторы 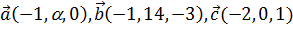. Определить значение a, при котором векторы  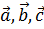компланарны.

 

Вариант 17

1. Вектор 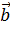 составляет с осями OX и OY углы α = 45ᵒ, γ = 45ᵒ. Вычислить его координаты при условии, что .

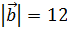2. Вектор 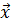 коллинеарен вектору  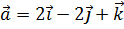и образует тупой угол с осью OZ. Зная, что 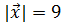, найти его координаты.

3. Найти длину вектора 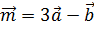, если , , .

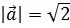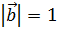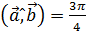4. Даны векторы 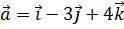,  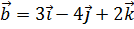и 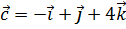. Найти проекцию вектора  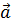на вектор .

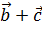5. Определить внутренний угол при вершине В треугольника АВС с вершинами А(2, -1, 3), В(1, 1, 1), С0, 0, 5).

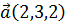6. Вектор  , перпендикулярный векторам  и 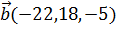, образует с осью ОХ тупой угол. Найти его координаты, если .

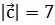7. Дан треугольник с вершинами А(3, -1, 4), В(2, 4, 2), С(4, 4, 4). Найти его площадь и длину высоты СN.

8. Даны три силы 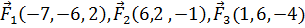, приложенные к точке B(3, 6,−1). Вычислить работу, производимую равнодействующей этих сил, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку C(−6, −2, 17).

9. Вершины пирамиды находятся в точках А1(7, 10, 3), А2(−2, 8, 2), А3(6, 8, 9), А4(10, 6, 6). Вычислить ее объем и длину высоты, опущенной из вершины А1 на грань А2А3А4.

10. При каком значении z точка N(−2, 1, z) ,будет лежать в плоскости точек А(−3, 4, −1), В(−2, −5, 0), С(1, −3, −2)?

 

Вариант 18

1. Известны модуль вектора 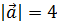 и два угла, образуемые им с координатными осями: a = 60°, g = 120°. Найти координаты вектора .

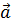2. Вектор  образует тупой угол с осью OХ и коллинеарен вектору 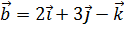. Найти координаты вектора, .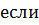

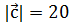3.

 

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.