Применение производной к исследованию функций (14 задание)

Стр 1 из 2Следующая ⇒

Применение производной к исследованию функций (14 задание)

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если 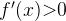, то функция 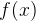возрастает.

Если 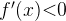, то функция 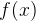убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

	возрастает	точка максимума	убывает	точка минимума	возрастает

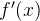
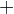
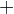
Производная функции 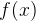в точке 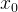равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

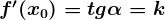
Производная — это скорость изменения функции.

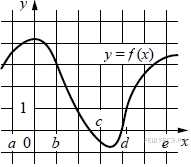
Пример: На рисунке изображён график функции y = f(x). Числа a, b, c, d и e задают на оси x четыре интервала. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной

ТОЧКИ

А) (a; b)

Б) (b; c)

В) (c; d)

Г) (d; e)

ЗНАЧЕНИЯ ПРОИЗВОДНОЙ

1) производная отрицательна на всём интервале

2) производная положительна в начале интервала и отрицательна в конце интервала

3) функция отрицательна в начале интервала и положительна в конце интервала

4) производная положительна на всём интервале

Решение: 1 - Если 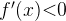, то функция 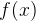убывает, подходят точки b и c;

2- положительна в начале, значит возрастает, отрицательна в конце, значит убывает – подходят точки а и b;

3 – отрицательна в начале, значит убывает, положительна в конце, значит возрастает – подходят точки c и d;

4 - 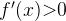, то функция 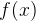возрастает, значит подходят точки d и e.

12 Следующая ⇒