Контакты

Случайная статья

Примеры решения задач

Тема. Ряды.

Решаете все задания варианта (номер варианта по последней цифре зачетной книжки ) высылаете на проверку задания б) на https://vk.com/id161843616 или https://vk.com/id545292512, или almazovamarina@gmail.com

Каждую высланную страницу нумеруете и подписываете.

Тема. Ряды.

Вопросы для самопроверки

1. Что называется числовым рядом.

2. Что такое сумма ряда.

3. Назовите необходимое условие сходимости ряда.

4. Какой ряд называется гармоническим?

5. Что значит, члены ряда образуют геометрическую прогрессию?

6. Какими свойствами обладают сходящиеся ряды?

7. Назовите признаки сравнения для рядов с положительными членами.

8. Сформулируйте признак Даламбера.

9. В чем заключается радикальный признак Коши?

10. В чем заключается интегральный признак Коши.

11. Какие ряды называются знакочередующимися?

Вариант1

1. Исследуйте ряд на сходимость:

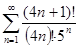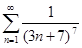а) б) в)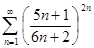

г)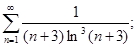

Вариант 2

1. Исследуйте ряд на сходимость:

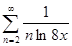а) б) в)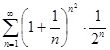

г)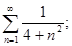

Вариант 3

1. Исследуйте ряд на сходимость:

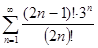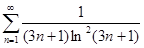а) б) в)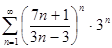

Г)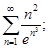

Вариант 4

1. Исследуйте ряд на сходимость:

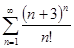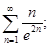а) б) в)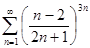

г)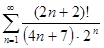

Вариант 5

1. Исследуйте ряд на сходимость:

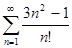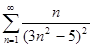а) б) в)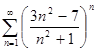

г)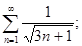

Вариант 6

1. Исследуйте ряд на сходимость:

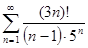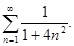а) б) в)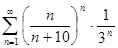

г)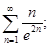

Вариант 7

1. Исследуйте ряд на сходимость:

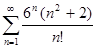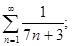а) б) в)

г)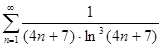

Вариант 8

1. Исследуйте ряд на сходимость:

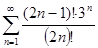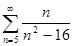а) б) в)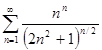

г)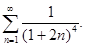

Вариант 9

1. Исследуйте ряд на сходимость:

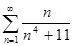а) б) в)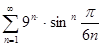

г)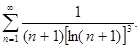

Вариант 10

1. Исследуйте ряд на сходимость:

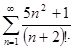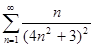а) б) в)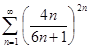

г)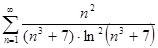

Примеры решения задач

Задача 8. Исследовать сходимость ряда

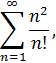
пользуясь признаком сходимости Даламбера.

Решение.Если дан ряд

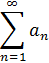
с положительными членам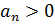и ( ) и

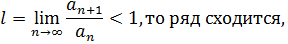
если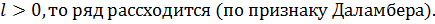

Для нашего ряда

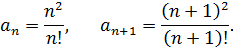
Найдем

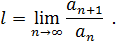
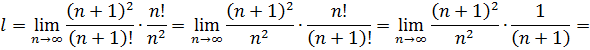
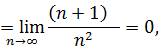
Итак 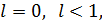следовательно, ряд сходится.

Задача 9. Исследовать сходимость ряда, пользуясь интегральным признаком сходимости Коши.

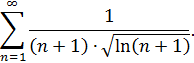
Решение. Рассмотрим несобственный интеграл

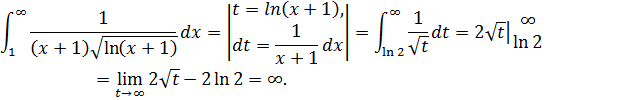
Этот несобственный интеграл расходится, следовательно, данный ряд расходится.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.