
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Рис.33. Колебания ма- тематического маятника.
§ 8-4. Колебания математического и физического маятников.
Из школьного курса физики известно, что математический маятник представляет собой точечную массу, подвешенную на длинной невесомой и нерастяжимой нити. На первый взгляд раскачивание такой системы связано с изменением
по меньшей мере двух координат сразу так, что для описания такого движения на-
до записывать второй закон Ньютона ( уравнение движения ) для каждой из координат в отдельности, а затем искать связь между ними. Однако задача может быть упрощена, если обратить внимание на то, что движение математического маятника происходит при постоянной длине нити подвеса, т.е. его можно рассматривать как частный случай вращательного движения, когда в качестве единственной переменной выбирается угол отклонения от положения равновесия. В этом случае вместо уравнения движения в форме второго закона Ньютона необходимо использовать основное уравнение динамики вращательного движения:
I 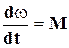 , ( 8-20)
, ( 8-20)
где I - момент инерции точечной массы относительно точки подвеса, М - момент
l j
h m
mg |
Рис.33. Колебания ма- тематического маятника.
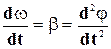 - угловое ускорение массы, которое, в свою очередь, определяется как вторая производная по времени от угла j отклонения от вертикали (см. рис. 33).
Момент инерции точечной массы m, находящейся на расстоянии l от оси вращения, по определению равен
I = m l2 , а единственной силой, момент которой относительно оси вращения отличен от нуля, является сила тяжести. Ее момент относительно оси, проходящей че-
- угловое ускорение массы, которое, в свою очередь, определяется как вторая производная по времени от угла j отклонения от вертикали (см. рис. 33).
Момент инерции точечной массы m, находящейся на расстоянии l от оси вращения, по определению равен
I = m l2 , а единственной силой, момент которой относительно оси вращения отличен от нуля, является сила тяжести. Ее момент относительно оси, проходящей че-

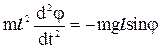 , ( 8-21)
, ( 8-21)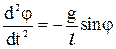 . ( 8-22 )
. ( 8-22 )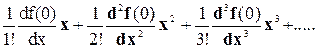
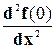 и синус угла j равен:
и синус угла j равен: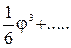
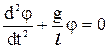 , ( 8-23 )
, ( 8-23 )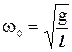 . ( 8-24)
. ( 8-24)





 О
l цм
j
mg
Рис.34. Физический
маятник.
О
l цм
j
mg
Рис.34. Физический
маятник.
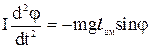 , ( 8-25)
где lцм обозначает расстояние, на котором расположен центр масс тела от оси вращения (см.рис.34). Однако те-
теперь момент инерции такого маятника требует специального вычисления, которого в рамках нашего курса
, ( 8-25)
где lцм обозначает расстояние, на котором расположен центр масс тела от оси вращения (см.рис.34). Однако те-
теперь момент инерции такого маятника требует специального вычисления, которого в рамках нашего курса
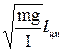 . ( 8-26)
. ( 8-26)