Хелпикс

Главная

Контакты

Случайная статья



математика ПАР-65. Тема: График и свойства функций tgx=y и ctgx = y



20.05.2020 математика ПАР-65

Тема: График и свойства функций tgx=y и ctgx = y

Изучение свойств функции y=tgx начнем с построения графика. Обратимся к единичной окружности:

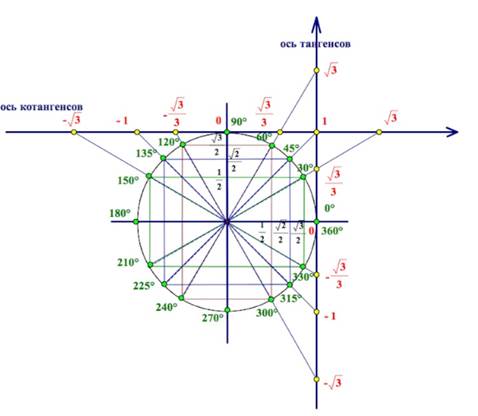
рис.1 Тригонометрический круг

Переносим основные значения углов на координатную плоскость. По оси абсцисс откладываем угол в радианах, по оси ординат – значения тангенса угла.

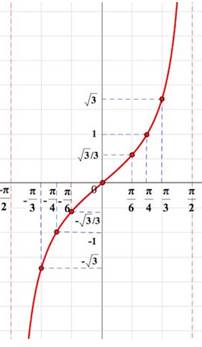
рис.2 График y=tgx на промежутке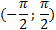

Как любая тригонометрическая функции, функция тангенса периодическая, делая параллельный перенос получаем:

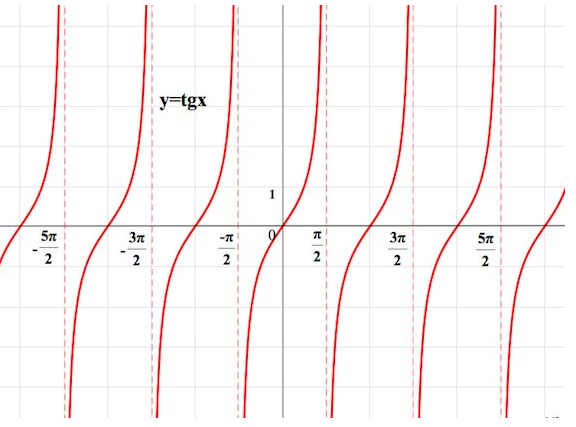
рис.3 График y=tgx

Заметим, что график симметричен относительно начала координат, следовательно функция тангенса нечётная. Используя построенный нами график, выведем основные свойства y=tgx:

1. Область определения функции y = tgx все действительные числа, кроме чисел вида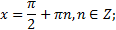

2. Функция периодическая с периодом , т.к.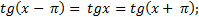

3. Функция нечётная, т.к. 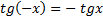. График нечётной функции симметричен относительно начала координат;

4. Функция возрастает на всём интервале;

5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;

6.

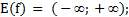
7. Функция 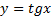принимает:

  • значение, равное 0, при ;
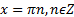  • положительные значения на интервале
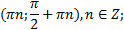
  • отрицательные значения на интервале

 

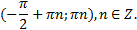
Для построения графика можно придерживаться алгоритму рассмотренному при построении графика 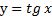, однако 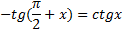(формула приведения). Т.е. смещая тангенсоиду на 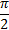единиц влево и делаем симметрию относительно оси Ох за счёт коэффициента –1, получаем:

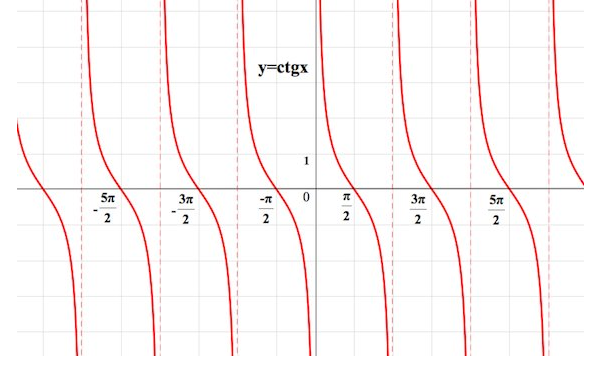
рис.3 График y=сtgx

Основные свойства y=сtgx:

1. Область определения функции y = сtgx все действительные числа, кроме чисел вида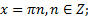

2. Функция периодическая с периодом ;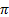

3. Функция нечётная. График нечётной функции симметричен относительно начала координат;

4. Функция убывает на всём интервале;

5. Функция не ограничена ни снизу, ни сверху. Функция не имеет ни наибольшего, ни наименьшего значений;

6. .

 

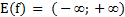Пример 1.

Найдем все корни уравнения 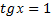, принадлежащие отрезку .

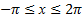Построим графики функци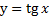й и 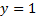(рис. 6)

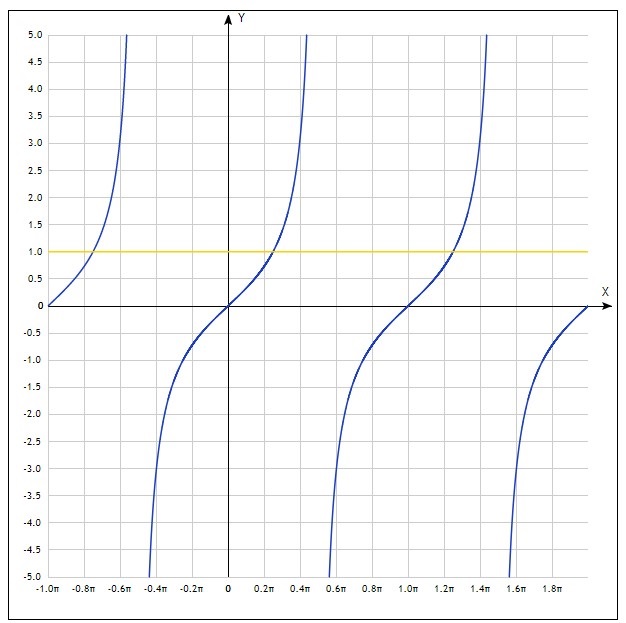
Рис. 4 – графики функци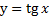й и .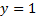

Графики пересекаются в трёх точках, абсциссы которых 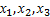являются корнями уравнения .

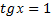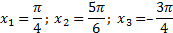
Ответ: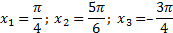

Пример 2.Найти все решения неравенства 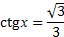, принадлежащие отрезку .

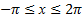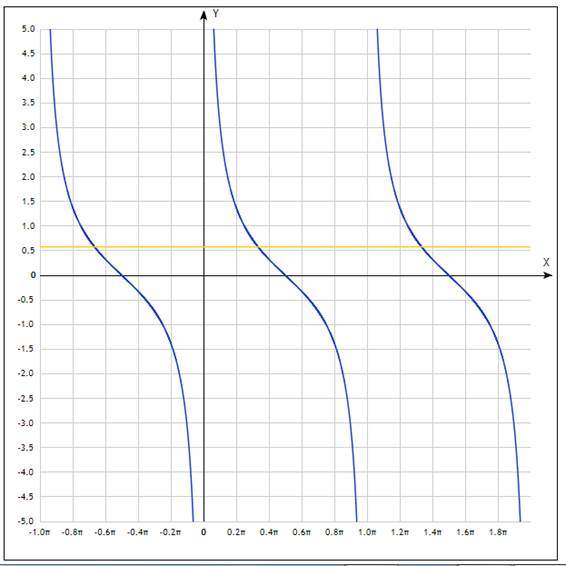
рис.5 графики функци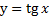й и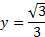

Графики пересекаются в трёх точках, абсциссы которых 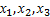являются корнями уравнения .

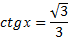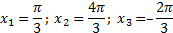
Ответ: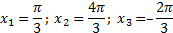

Домашнее задание:

1.Используя графики функций у = tg x и у = ctg х, найти наименьшие положительные корни уравнений:

 

a) tg х = —3; б) tg х = 2; в) ctg х = —3; г) ctg x = 2.

 

2. Используя графики функций у = tg x и у = ctg х, найти все корни уравнений:

 

a) tg х = \/3; б) ctg x = 1 / \/ 3

 
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.