
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
2016-2017 оқу жылына «Математика 2» пәні бойынша тест сұрақтары
⇐ ПредыдущаяСтр 2 из 2
Мамандықтар: 5В070800 – «Мұнай-газ ісі»
Оқыту тілі- қазақша, семестр-2, курс-1
Топтар:НГД-11,13
Тест сұрақтарын дайындауға жауапты оқытушылар – Уразгалиева А.Н.
| № п.п | Қиындық деңгейі | Сұрақтар | тақырыбы | А) (Дұрыс жауап) | В) (Дұрыс жауап) | С) (Дұрыс жауап) | D) | Е) | F) | G) | H) |
| 1. | 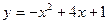 функциясының экстремум нүктелерін табу керек. функциясының экстремум нүктелерін табу керек.
| 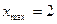
| 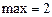
| 
| 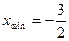
| 
| 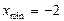
| 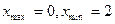
| |||
| 2. | 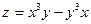 функциясының дербес туындыларын табыңыз. функциясының дербес туындыларын табыңыз.
| 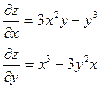
| 
| 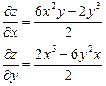
| 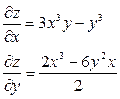
| 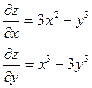
| 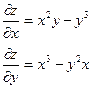
| 
| 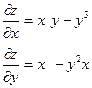
| ||
| 3. |  функциясының х( функциясының х( 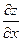 ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте. ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте.
| 
| 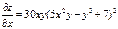
| 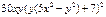
| 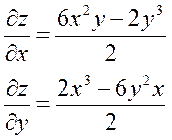
| 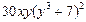
| 
| 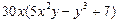
| 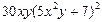
| ||
| 4. |  функциясының у( функциясының у(  ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте. ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте.
| 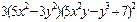
| 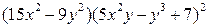
| 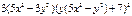
| 
| 
| 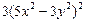
| 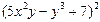
| 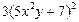
| ||
| 5. | z=  функциясының х( функциясының х( 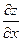 ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте. ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте.
| 
| 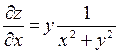
| 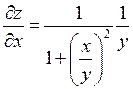
| 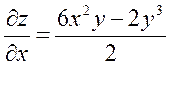
| 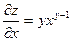
| 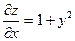
| 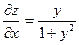
| 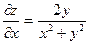
| ||
| 6. | z=  функциясының у( функциясының у(  ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте. ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте.
| 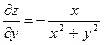
| 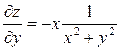
| 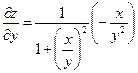
| 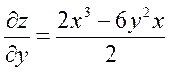
| 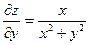
| 
| 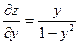
| 
| ||
| 7. | 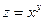 функциясының дербес туындыларын табыңыз. функциясының дербес туындыларын табыңыз.
| 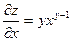 ; ; 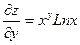
| 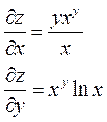
| 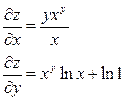
| 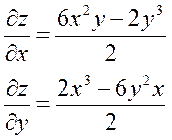
| 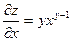 ; ; 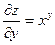
| 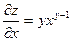 ; ; 
| 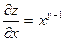 ; ; 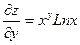
| 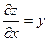

| ||
| 8. | 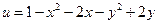 функциясының функциясының 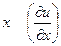 айнымалысы бойынша 1-ші ретті дербес туындысын есепте. айнымалысы бойынша 1-ші ретті дербес туындысын есепте.
| 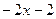
| 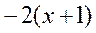
| 
| 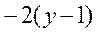
| 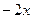
| 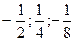
| 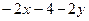
| |||
| 9. | 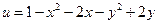 функциясының у( функциясының у( 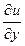 ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте. ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте.
| -2у+2 | 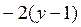
| 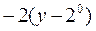
| 
| 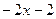
| 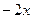
| 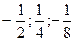
| 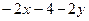
| ||
| 10. |  функциясының функциясының 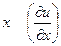 айнымалысы бойынша 1-ші ретті дербес туындысын есепте. айнымалысы бойынша 1-ші ретті дербес туындысын есепте.
| 2х+2 | 
| 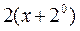
| 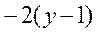
| 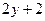
| 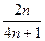
| 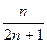
| |||
| 11. |  функциясының у( функциясының у( 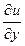 ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте. ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте.
| 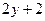
| 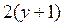
|
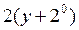
| 
| 
| 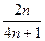
| 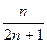
| |||
| 12. | 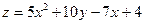 функциясының функциясының 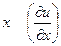 айнымалысы бойынша 1-ші ретті дербес туындысын есепте. айнымалысы бойынша 1-ші ретті дербес туындысын есепте.
| 10х-7 | 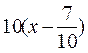
| 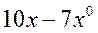
| 
| 24х+24-7 | 24х | 24y | |||
| 13. |  функциясының у( функциясының у( 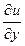 ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте. ) айнымалысы бойынша 1-ші ретті дербес туындысын есепте.
| 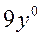
| 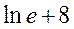
| 2x | 2x+y | 2y | X2+9 | ||||
| 14. | 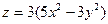 функциясының дербес туындыларын табыңыз. функциясының дербес туындыларын табыңыз.
| 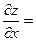 30х , 30х , 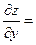 -18у -18у
| 
| 
| 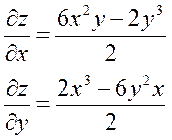
| 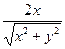
| 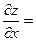 30x 30x
| 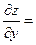 18у 18у
| 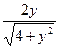
| ||
| 15. | 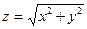 функциясының функциясының 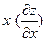 айнымалысы бойынша 1-ші ретті дербес туындысын есепте. айнымалысы бойынша 1-ші ретті дербес туындысын есепте.
| 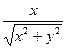
| 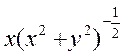
| 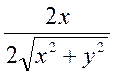
| 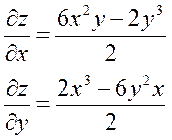
| 
| 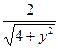
| 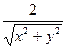
| 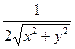
| ||
| 16. | 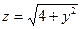 функциясының функциясының 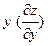 айнымалысы бойынша 1-ші ретті дербес туындысын есепте айнымалысы бойынша 1-ші ретті дербес туындысын есепте
| 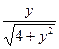
| 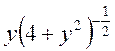
| 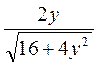
| 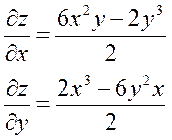
| 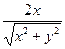
| 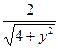
| 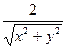
| 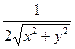
| ||
| 17. | 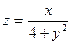 функциясының дербес туындыларын табыңыз. функциясының дербес туындыларын табыңыз.
| 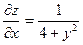 , , 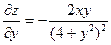
| 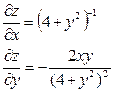
| 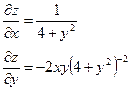
| 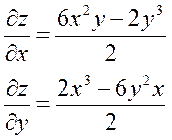
| 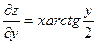
| 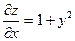
| 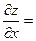 30x 30x
| 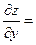 18у 18у
| ||
| 18. | 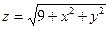 функциясының дербес туындыларын табыңыз. функциясының дербес туындыларын табыңыз.
| 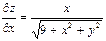 , , 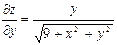
| 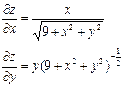
| 
| 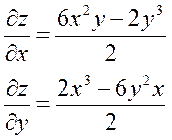
|  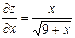
| 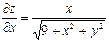 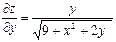
| 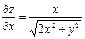 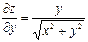
| 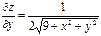 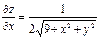
| ||
| 19. | 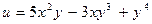 функциясының кез-келген нүктедегі градиентінің проекцияларын табыңыз. функциясының кез-келген нүктедегі градиентінің проекцияларын табыңыз.
| 
| 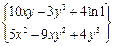
| 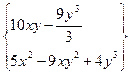
| 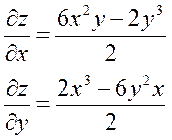
| 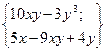
| 
| 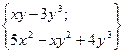
| 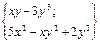
| ||
| 20. | 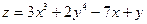 функциясының кез-келген нүктедегі градиентінің проекцияларын табыңыз. функциясының кез-келген нүктедегі градиентінің проекцияларын табыңыз.
| {9x2-7; 8y3+1} | 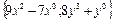
| 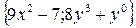
| 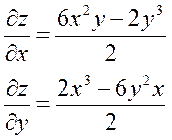
| 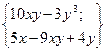
| {9x2;8y3+1} | {9x2 ; 8y3} | {9x2-7; 8y3} | ||
| 21. |  функциясының кез-келген нүктедегі градиентінің проекцияларын табыңыз. функциясының кез-келген нүктедегі градиентінің проекцияларын табыңыз.
| {3; -10y+7} | 
| 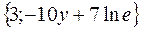
| 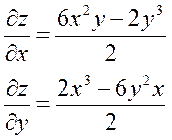
| {3; -24} | {3х; -24y+7} | {3х; -24y} | {3; -24y-7} | ||
| 22. |  (1;2) нүктесіндегі градиентін табу керек. (1;2) нүктесіндегі градиентін табу керек.
| {-2;1} | 
| 
| 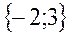
| {-4;5} | {-3;-4} | {-1;4} | {-2;4} | ||
| 23. |  . (2,1) нүктесіндегі градиентін табу керек. . (2,1) нүктесіндегі градиентін табу керек.
| {3,-1} | 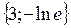
| 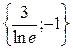
| 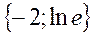
| {-4;5} | {-2;1} | {-3;-4} | {-2;4} | ||
| 24. | 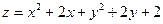 . (1,1) нүктесіндегі градиентін табу керек. . (1,1) нүктесіндегі градиентін табу керек.
| {4,4} | 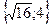
|
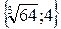
| 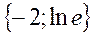
| {-2;1} | {-3;-4} | {-4;5} | {-2;4} | ||
| 25. |  функциясының (3;2) нүктесіндегі функциясының (3;2) нүктесіндегі 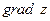 -ті табу керек. -ті табу керек.
| 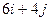
| 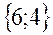
| 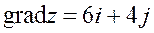
| 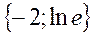
| 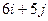
| 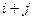
| 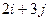
| 
| ||
| 26. | 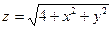 функциясының (2;1) нүктесіндегі функциясының (2;1) нүктесіндегі 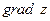 -ті табу керек. -ті табу керек.
| 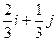
| 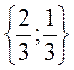
| 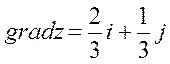
| 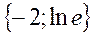
| 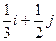
| 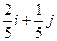

| 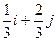
| 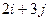
| ||
| 27. | 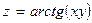 функциясының (1;1) нүктесіндегі бірінші координаттық бұрыштың биссектрисасының бағытымен алынған туындысын табу керек. функциясының (1;1) нүктесіндегі бірінші координаттық бұрыштың биссектрисасының бағытымен алынған туындысын табу керек.
| 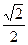
| 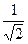
| 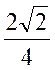
| 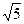
| 
| 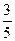
| 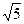 +2 +2
| |||
| 28. |  функциясының М(3;1) нүктесіндегі, осы нүктеден (6;5) нүктесіне қарай бағытталған туындысын табу керек. функциясының М(3;1) нүктесіндегі, осы нүктеден (6;5) нүктесіне қарай бағытталған туындысын табу керек.
| 
| 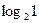
| -1 | -2 | ||||||
| 29. | 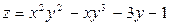 функциясының (2;1) нүктесіндегі, осы нүктеден координаталар басына қарай бағытталған туындысын табу керек. функциясының (2;1) нүктесіндегі, осы нүктеден координаталар басына қарай бағытталған туындысын табу керек.
| - 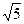
| 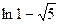
| 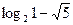
| 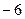
| 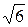
| |||||
| 30. | Дифференциалдық теңдеу дегеніміз, нені байланыстыратын теңдеу? | 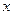 - тәуелсіз айнымалы - тәуелсіз айнымалы
| 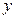 - ізделінді функция - ізделінді функция
| Функцияның барлық ретті туындыларын | Түрлі функцияларды | 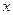 тәуелсіз айнымалысы бар теңдеу тәуелсіз айнымалысы бар теңдеу
| 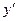 туындысы бар теңдеу туындысы бар теңдеу
| 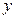 ізделінді функциясы бар теңдеу ізделінді функциясы бар теңдеу
| Тәуелсіз айнымалы 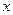 және ізделінді функцияны және ізделінді функцияны 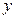 байланыстыратын теңдеу байланыстыратын теңдеу
| ||
| 31. | 2-ретті дифференциалдық теңдеуді табыңыз? | 
| 
| 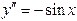
| 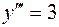
| 
| 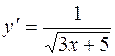
| 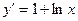
| 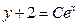
| ||
| 32. | Дифференциалдық теңдеудің шешімін тап: 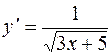
| 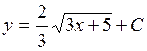
| 
| 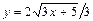
| 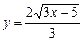
| 
| 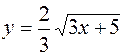
| 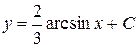
| 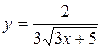
| ||
| 33. | Дифференциалдық теңдеудің шешімін тап: 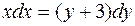
| 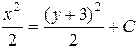
| 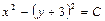
| 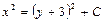
| 
| 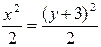
| 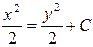
| 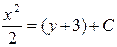
| 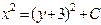
| ||
| 34. | Дифференциалдық теңдеудің шешімін тап: 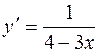
| 
| 
| 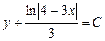
| 
| 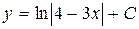
| 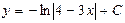
| 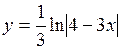
| 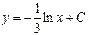
| ||
| 35. | Дифференциалдық теңдеудің шешімін тап: 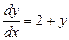
| 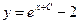
| 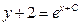
| 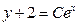
| 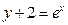
| 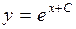
| 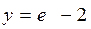
| 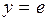
| 
| ||
| 36. | Дифференциалдық теңдеудің шешімін тап: 
| 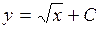
| 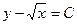
| 
| 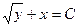
| 
| 
| 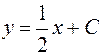
| 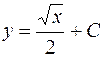
| ||
| 37. | Дифференциалдық теңдеудің шешімін тап: 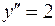
| 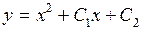
| 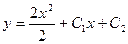
| 
| 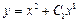
| 
| 
| 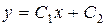
| 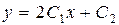
| ||
| 38. | Дифференциалдық теңдеудің шешімін тап: 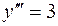
| 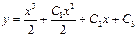
| 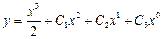
| 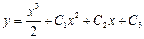
| 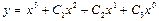
| 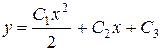
| 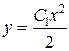
| 
| 
| ||
| 39. | Дифференциалдық теңдеудің шешімін тап: 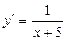
| 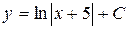
| 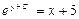
| 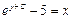
| 
| 
| 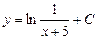
| 
| 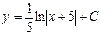
| ||
| 40. | Дифференциалдық теңдеудің шешімін тап: 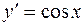
| 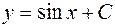
| 
| 
| 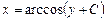
| 
| 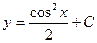
| 
| 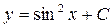
| ||
| 41. | Дифференциалдық теңдеудің шешімін тап: 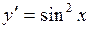
| 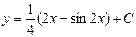
| 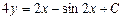
| 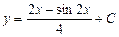
| 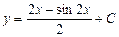
| 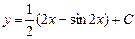
| 
| 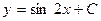
| 
| ||
| 42. | Дифференциалдық теңдеудің шешімін тап: 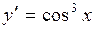
| 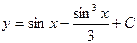
| 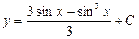
| 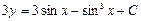
| 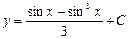
| 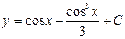
| 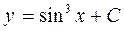
| 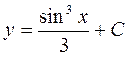
| 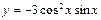
| ||
| 43. | Дифференциалдық теңдеудің шешімін тап: 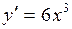
| 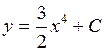
| 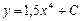
| 
| 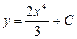
| 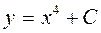
| 
| 
| 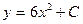
| ||
| 44. | Дифференциалдық теңдеудің шешімін тап: 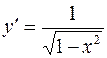
| 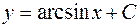
| 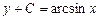
| 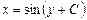
| 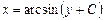
| 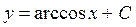
| 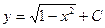
| 
| 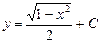
| ||
| 45. | Дифференциалдық теңдеудің шешімін тап:

| 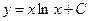
| 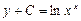
| 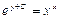
| 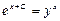
| 
| 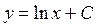
| 
| 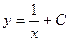
| ||
| 46. | Дифференциалдық теңдеуді шешіңіз: 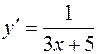
| 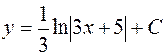
| 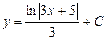
| 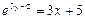
| 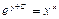
| 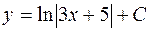
| 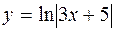
| 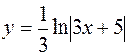
| 
| ||
| 47. | Дифференциалдық теңдеуді шешіңіз: 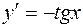
| 
| 
| 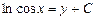
| 
| 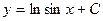
| 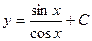
| 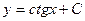
| 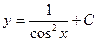
| ||
| 48. | Дифференциалдық теңдеуді шешіңіз: 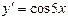
| 
| 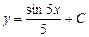
| 
| 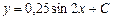
| 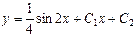
| 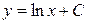
| 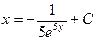
| 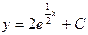
| ||
| 49. | Дифференциалдық теңдеуді шешіңіз: 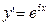
| 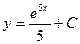
| 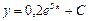
| 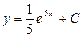
| 
| 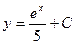
| 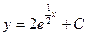
| 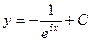
| 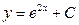
| ||
| 50. | Дифференциалдық теңдеуді шешіңіз: 
| 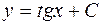
| 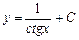
| 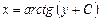
| 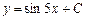
| 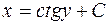
| 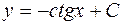
| 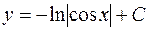
| 
| ||
| 51. | Дифференциалдық теңдеуді шешіңіз: 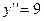
| 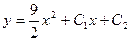
| 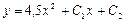
| 
| 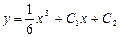
| 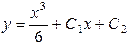
| 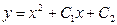
| 
| 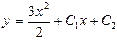
| ||
| 52. | Дифференциалдық теңдеуді шешіңіз: 
| 
| 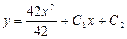
| 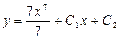
| 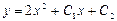
| 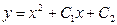
| 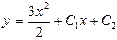
| 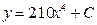
| 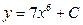
| ||
| 53. | Дифференциалдық теңдеуді шешіңіз: 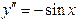
| 
| 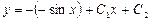
| 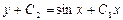
| 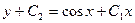
| 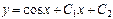
| 
| 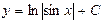
| 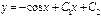
| ||
| 54. | Дифференциалдық теңдеуді шешіңіз: 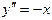
| 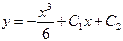
| 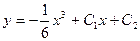
| 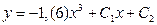
| 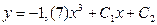
| 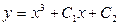
| 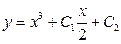
| 
| 
| ||
| 55. | к –ның қандай мәнінде 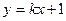 функциясы функциясы 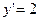 теңдеуінің шешімі болады. теңдеуінің шешімі болады.
| 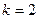
| 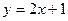
| 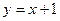
| 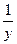
| 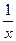
| |||||
| 56. | к-ның мәнінде 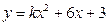 функциясы функциясы  теңдеуінің шешімі болады. теңдеуінің шешімі болады.
| 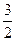
| 1,5 | 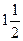
| 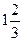
| 1,3 | -3 | 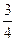
| |||
| 57. | Дифференциалдық теңдеуді шешіңіз: 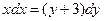
| 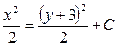
| 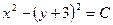
| 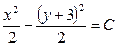
| 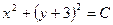
| 
| 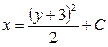
| 
| 
| ||
| 58. | Дифференциалдық теңдеуді шешіңіз: 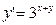
| 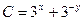
| 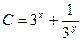
| 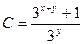
| 
| 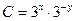
| 
| 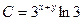
| 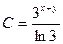
| ||
| 59. | Дифференциалдық теңдеуді шешіңіз: 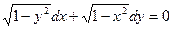
| 
|  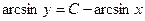
| 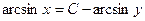
| 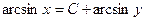
| 
| 
| 
| 
| ||
| 60. | Дифференциалдық теңдеуді шешіңіз: 
| 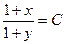
| 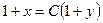
| 
| 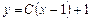
| 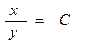
| 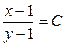
| 
| 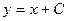
| ||
| 61. | Дифференциалдық теңдеуді шешіңіз: 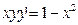
| 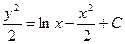
| 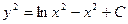
| 
| 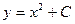
| 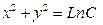
| 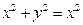
| 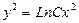
| 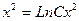
| ||
| 62. | Дифференциалдық теңдеуді шешіңіз: 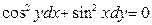
| 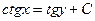
| 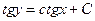
| 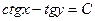
| 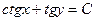
| 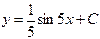
| 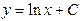
| 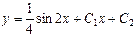
| 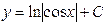
| ||
| 63. | 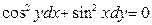 . Дифференциалдық теңдеуінің ретін көрсетіңіз. . Дифференциалдық теңдеуінің ретін көрсетіңіз.
| I | бірінші | екінші | |||||||
| 64. | 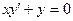 теңдеуі қандай түрге жатады? теңдеуі қандай түрге жатады?
| Айнымалылары ажыратылатын | Бірінші ретті | Дифференциалдық теңдеу | Интегралдық теңдеу | Толық дифференциалдық теңдеу | Бернулли теңдеуі | Квадрат теңдеу | Біртекті | ||
| 65. | 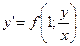 теңдеудің түрін көрсетіңіз. теңдеудің түрін көрсетіңіз.
| Біртекті | Бірінші ретті | Дифференциалдық теңдеу | Интегралдық теңдеу | Толық дифференциалдық теңдеу | Бернулли теңдеуі | Квадрат теңдеу | Айнымалылары ажыратылатын | ||
| 66. | Теңдеудің түрін к&#
|
||||||||||
|