
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ВЕКТОРНАЯ АЛГЕБРА
2. ВЕКТОРНАЯ АЛГЕБРА
| Наименование | Обозначение, формула |
| Вектор и его выражение в декартовых координатах | a=axi+ayj+azk=(ax,ay,az) |
| Модуль (длина) вектора |  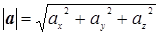
|
| Направляющие косинусы вектора | 
|
| Сложение двух векторов | a+b=(ax+bx,ay+by,az+bz) |
| Умножение вектора на скаляр | ka=(kax,kay,kaz) |
| Скалярное произведение двух векторов | 
|
| Скалярное произведение в декартовых координатах | ab=axbx+ayby+azbz |
| Условие ортогональности двух ненулевых векторов | ab=0 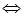 a^b a^b
|
| Векторное произведение двух векторов | 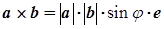
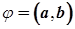 , e^a, e^b
e - единичный вектор
a, b, e - правая тройка векторов , e^a, e^b
e - единичный вектор
a, b, e - правая тройка векторов
|
| Векторное произведение в декартовых координатах | 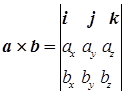
|
| Условие коллинеарности двух ненулевых векторов |  a||b a||b
|
| Смешанное произведение трех векторов | 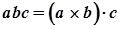
|
| Смешанное произведение в декартовых координатах | 
|
| Условие компланарности трех ненулевых векторов | abc=0 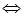 a, b, c -компланарны (лежат в одной плоскости) a, b, c -компланарны (лежат в одной плоскости)
|
| Линейно независимая система векторов | {a1,a2,…,an} - линейно независима 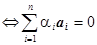 только при условии только при условии 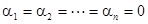 . .
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|