Движение шарика по наклонной плоскости.

Движение шарика по наклонной плоскости.

Дана наклонная плоскость, по которой скатывается шарик:

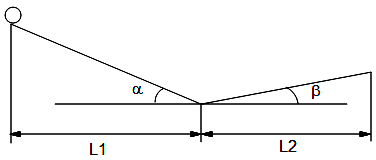
α=20⁰

β=40⁰

L₁= 3 м

kтр₁ = 0,022

kтр₂ = 0,3

Сопротивлением воздуха пренебрегаем.

Построим модель движения шарика.

На начальном этапе шарик движется по наклонной плоскости длиной L₁, расположенной под углом α. Коэффициент трения при движении шарика по наклонной плоскости описывается величиной kтр₁. Затем шарик движется по наклонной плоскости с углом наклона β вверх. Коэффициент трения kтр₂.

При спуске с наклонной плоскости и отсутствии дополнительных сил ускорение равно a₁ = g*(sin( α)- kтр₁ * cos (α)), где g - ускорение свободного падения. Поскольку начальная скорость шарика равна нулю, скорость шарика v = a₁*t. Путь, который пройдёт шарик, равен L₁ = a₁*t²/2. Отсюда t = 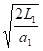. Значит, скорость шарика в момент прохождения отрезка пути L₁ составит v = a₁* t = .

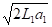Далее шарик движется по наклонной плоскости вверх. При подъеме по наклонной плоскости и отсутствии дополнительных сил a₂ = g*(sin(β) + kтр₂ * cos (β)). Поскольку у шарика уже есть начальная скорость v, пройденный путь составит: L₂ = v*t₂ + a₂*(t₂)²/2. Нам необходимо найти максимальный пройденный путь. В момент остановки шарика ускорение равно 0. Время подъёма. t₂= v / a₂. Тогда пройденный путь равен L₂ = v*t₂ = v²/a₂.

Математическая модель построена.

Построить модель в MS Office Excel.

Параметр	Значение	Ед. измерения
Угол α
Угол β
kтр₁
kтр₂
g
a₁
a₂
v
L₁
L₂

Для этого в соответсвующие пустые ячейки занести заданные значения или соответсвующие формулы.

Построить график зависимости L₁(α) для 10⁰< α<40⁰