
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Рабочий лист.. Тема: «Координаты и векторы». Вариант 1А
Рабочий лист.
| Предмет | Математика |
| Группа | № 5 2 курс |
| Тема урока | Проверочная работа «Координаты и векторы» |
| ФИО преподавателя | Тимиршина Алия Мунзиловна |
| Где находится задание: | |
| Учебник | |
| Ссылка | |
| Сроки выполнения задания | 24.09.2020 до 17:00 |
| Как выполнять задание | Выполнить указанный вариант работы. |
| Домашняя работа | Выполнить любой другой вариант. |
| Обратная связь | Выполненные работы отправить личным сообщением ВК |
| Как узнать отметку о выполненном задании | Оценки будут выставлены в личный журнал преподавателя и отправлены в беседу ВК. |
Распределение вариантов
| № | ФИО | Вариант |
| Акиев Владимир Петрович | 1С | |
| Васильев Александр Сергеевич | 1А | |
| Гарипов Рамиль Игоревич | 2А | |
| Гильмуллин Артур Ильдарович | 1А | |
| Гильмияров Никита Игоревич | 2В | |
| Давлетханова Эльвира Рамазановна | 1А | |
| Ильчигулова Лада Алексеевна | 1С | |
| Ильчибаев Владислав Вячеславович | 1А | |
| Калитов Кирилл Русланович | 1С | |
| Кумушбаева Валерия Владиславовна | 1С | |
| Рашитов Даниил Борисович | 2А | |
| Салихов Александр Андреевич | 2А | |
| Сафиуллин Ильнар Ильясович | 2В | |
| Стрелецкий Владлен Владимирович | 1В | |
| Суфияров Рамазан Рамисович | 2А | |
| Суханов Данил Олегович | 1В | |
| Тетюцкий Никита Анатольевич | 1А | |
| Тимербаева Арина Михайловна | 2В | |
| Хафизов Ильназ Альфретович | 1С | |
| Шаймарданов Николай Борисович | 2В | |
| Шарипзянов Эмиль Фанисович | 1С | |
| Янгиров Артем Ильдарович | 1А |
Тема: «Координаты и векторы»
Вариант 1А
1. Даны точки: А(2;-4;0), В(0;5;0), С(7;0;-5), D(3;4;5), Е(0;0; -7). Укажите среди них точки, которые лежат на оси у:
а) С б) А в) В г) Е
2. Даны точки А(2;-1;0) и В (-4;5;2). Найдите координаты середины отрезка АВ:
а) (-1;2;1) б) (-4;5;2) в) (-4;0;2) г) (0;5;2).
3.Дан вектор  (-2;3;1). Найдите вектор 2
(-2;3;1). Найдите вектор 2  :
:
а) 2  (4;6;-2) б) 2
(4;6;-2) б) 2  (-4;6;2) в) 2
(-4;6;2) в) 2  (4;0;-2) г) 2
(4;0;-2) г) 2  (0;6;-2)
(0;6;-2)
4. Дан вектор  (-2;3;1)
(-2;3;1)  (4;-1;2). Найдите вектор
(4;-1;2). Найдите вектор  +
+  :
:
а) (2;2;7) б) (-2;2;7) в) (2;2;3) г) (2;0;7)
5. Найдите длину вектора АВ, если А(0;1;-1) и В(1;-1;2),
а) 2 б) 5 в)7 г) 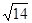
6. Даны четыре точки А(2;7;-3), В(1;0;3), С( -3;-4;5), D(-2;3;-1). Укажите среди векторов 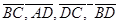 равные:
равные:
а) 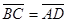 б)
б) 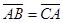 в)
в) 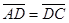 г)
г) 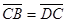
7. Дан вектор  (-2;3;1)
(-2;3;1)  (4;-1;2). Найдите вектор
(4;-1;2). Найдите вектор  -
-  :
:
а) (2;2;7) б) (-2;2;7) в) (-6;4;-1) г) (2;0;7)
8. Координата точки при переходе от плоскости к пространству задается: 
а) Р(х,y,z ) б) P(x,y) в) P(x,z) г) P(x)
9. Укажите формулу координаты середины отрезка:
а) 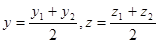 б)
б) 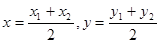
в) 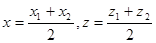 г)
г) 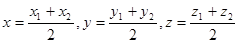
10. Плоскость задана уравнением:
а) 8y -3d =0 б) -8x +4y -7z -3=0 в) 9x +7y =0 г) 2x -3 =0
Вариант2А
1. Даны точки: А(2;-4;0), В(0;5;0), С(7;0;-5), D(3;4;5), Е(0;0; -7). Укажите среди них точки, которые лежат на оси z:
а) С б) А в) В г) Е
2. Даны точки А(0;-1;0) и В (-4;5;2). Найдите координаты середины отрезка АВ:
а) (-2;2;1) б) (-4;5;2) в) (-4;0;2) г) (0;5;2).
3.Дан вектор  (-2;3;1). Найдите вектор 3
(-2;3;1). Найдите вектор 3  :
:
а) 3  (4;6;-2) б) 3
(4;6;-2) б) 3  (-6;9;3) в) 3
(-6;9;3) в) 3  (4;0;-2) г) 3
(4;0;-2) г) 3  (0;6;-2)
(0;6;-2)
4. Дан вектор  (-2;4;0)
(-2;4;0)  (4;-1;2). Найдите вектор
(4;-1;2). Найдите вектор  +
+  :
:
а) (2;2;7) б) (-2;2;7) в) (2;3;2) г) (2;0;7)
5. Найдите длину вектора АВ, если А(0;6;-1) и В(2;-1;2),
а) 2 б) 5 в)7 г) 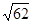
6. Даны четыре точки А(2;7;-3), В(1;0;3), С( -3;-4;5), D(-2;3;-1). Укажите среди векторов 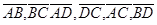 равные:
равные:
а) 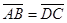 б)
б) 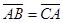 в)
в) 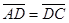 г)
г) 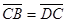
7. Дан вектор  (-2;0;1)
(-2;0;1)  (4;-1;0). Найдите вектор
(4;-1;0). Найдите вектор  -
-  :
:
а) (2;2;7) б) (-2;2;7) в) (-6;1;1) г) (2;0;7)
8.Укажите формулу по которой находят расстояние между точками:
а) 2x -4y +6z -3=0 б) 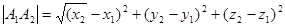
в) 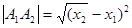 г)
г) 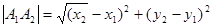
9. Координата точки при переходе от плоскости к пространству задается: 
а) Р(х,y,z ) б) P(x,y) в) P(x,z) г) P(x)
10. Плоскость задана уравнением:
а) 8y -3d =0 б)2x -4y +6z -3=0 в) 9x +7y =0 г) 2x -3 =0
Вариант 1В
1. Даны точки: А(2;-4;0), В(0;5;0), С(7;0;-5), D(3;4;5), Е(0;0; -7). Укажите среди них точки, которые лежат на плоскости ху:
а) С б) А в) В г) Е
2. Даны точки А(2;-1;0) и В (-4;7;2). Найдите координаты середины отрезка АВ:
а) (-1;3;1) б) (-4;5;2) в) (-4;0;2) г) (0;5;2).
3.Дан вектор  (1;-1;2). Найдите вектор 3
(1;-1;2). Найдите вектор 3  :
:
а) 3  (3;-3;6) б) 3
(3;-3;6) б) 3  (-4;6;2) в) 3
(-4;6;2) в) 3  (4;0;-2) г) 3
(4;0;-2) г) 3  (0;6;-2)
(0;6;-2)
4. Дан вектор  (-2;3;0)
(-2;3;0)  (4;-1;4). Найдите вектор
(4;-1;4). Найдите вектор  +
+  :
:
а) (2;2;7) б) (-2;2;7) в) (2;2;4) г) (2;0;7)
5. Найдите длину вектора АВ, если А(0;1;-2) и В(1;-1;2),
а) 2 б) 5 в)7 г) 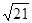
6. Даны четыре точки А(2;7;-3), В(1;0;3), С( -3;-4;5), D(-2;3;-1). Укажите среди векторов 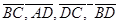 равные:
равные:
а) 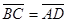 б)
б) 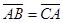 в)
в) 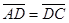 г)
г) 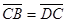
7. Дан вектор  (-2;3;3)
(-2;3;3)  (2;-1;2). Найдите вектор
(2;-1;2). Найдите вектор  -
-  :
:
а) (2;2;7) б) (-2;2;7) в) (-4;4;1) г) (2;0;7)
8. Координаты точки при переходе от плоскости к пространству задается: 
а) Р(х,y,z ) б) P(x,y) в) P(x,z) г) P(x)
9. Уравнение сферы задана формулой:
а) (х-а)2+ (у-b)2 +(z-c)2=R2 б) у=kx+b в)y=x2+ax г)y=x3+ax+b
10. Плоскость задана уравнением:
а) 8y -3d =0 б)2x -3y +5z -6=0 в) 9x +7y =0 г) 2x -3 =0
Вариант2В
1. Даны точки: А(2;-4;0), В(0;5;0), С(7;0;-5), D(3;4;5), Е(0;0; -7). Укажите среди них точки, которые лежат на плоскости хz:
а) С б) А в) В г) Е
2. Даны точки А(2;-2;0) и В (-4;6;2). Найдите координаты середины отрезка АВ:
а) (-1;2;1) б) (-4;5;2) в) (-4;0;2) г) (0;5;2).
3.Дан вектор  (1;-1;2). Найдите вектор 2
(1;-1;2). Найдите вектор 2  :
:
а) 2  (2;-2;4) б) 2
(2;-2;4) б) 2  (-4;6;2) в) 2
(-4;6;2) в) 2  (4;0;-2) г) 2
(4;0;-2) г) 2  (0;6;-2)
(0;6;-2)
4. Дан вектор  (-2;3;1)
(-2;3;1)  (4;0;-2). Найдите вектор
(4;0;-2). Найдите вектор  +
+  :
:
а) (2;2;7) б) (-2;2;7) в) (2;3;-1) г) (2;0;7)
5. Найдите длину вектора АВ, если А(3;0;-1) и В(1;-3;1),
а) 2 б) 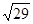 в)√17 г)
в)√17 г) 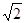
6. Даны четыре точки А(2;7;-3), В(1;0;3), С( -3;-4;5), D(-2;3;-1). Укажите среди векторов 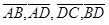 равные:
равные:
а) 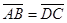 б)
б) 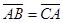 в)
в) 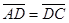 г)
г) 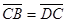
7. Дан вектор  (-2;2;1)
(-2;2;1)  (0;-1;2). Найдите вектор
(0;-1;2). Найдите вектор  -
-  :
:
а) (2;2;7) б) (-2;2;7) в) (-2;3;-1) г) (2;0;7)
8. Окружность задана уравнением:
а) (х-а)2+ (у-b)2 =R2 б) у=kx+b в)y=x2+ax г)y=x3+ax+b
9.Укажимте формулу по которой находят расстояние между точками:
а) 2x -4y +6z -3=0 б) 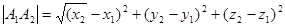
в) 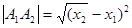 г)
г) 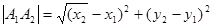
10. Плоскость задана уравнением:
а) 8y -3d =0 б) 9x -5y +6z -6=0 в) 9x +7y =0 г) 2x -3 =0
Вариант1С
1. Даны точки: А(2;-4;0), В(0;5;0), С(7;0;-5), D(3;4;5), Е(0;0; -7). Укажите среди них точки, которые лежат на плоскости хуz:
а) С б) А в) В г) D
2. Даны точки А(2;-3;0) и В (-4;5;6). Найдите координаты середины отрезка АВ:
а) (-1;1;3) б) (-4;5;2) в) (-4;0;2) г) (0;5;2).
3.Дан вектор  (1;-1;2). Найдите вектор 4
(1;-1;2). Найдите вектор 4  :
:
а) 4  (4;-4;8) б) 2
(4;-4;8) б) 2  (-4;6;2) в) 2
(-4;6;2) в) 2  (4;0;-2) г) 2
(4;0;-2) г) 2  (0;6;-2)
(0;6;-2)
4. Дан вектор 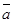 (-2;3;1)
(-2;3;1)  (4;0;2). Найдите вектор 2
(4;0;2). Найдите вектор 2 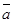 +
+  :
:
а) (2;2;7) б) (-2;2;7) в) (0;6;4) г) (2;0;7)
5. Найдите длину вектора АВ, если А( 2;1;-1) и В(1;-1;3),
а) 2 б) 5 в)7 г) 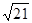
6. Даны четыре точки А(2;7;-3), В(1;0;3), С( -3;-4;5), D(-2;3;-1). Укажите среди векторов 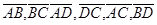 равные:
равные:
а) 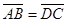 и
и 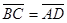 б)
б) 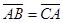 в)
в) 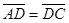 г)
г) 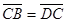
7. Дан вектор 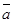 (-4;3;1)
(-4;3;1)  (4;-1;0). Найдите вектор
(4;-1;0). Найдите вектор 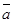 -
-  :
:
а) (2;2;7) б) (-2;2;7) в) (-8;4;1) г) (2;0;7)
8. Уравнение сферы задана формулой:
а) (х-а)2+ (у-b)2 +(z-c)2=R2 б) у=kx+b в)y=x2+ax г)y=x3+ax+b
9. Найдите косинус угла между векторами АВ и СD, если А(0;1;-1), В(1;-1;2), С( 3;1;0), D(2;-3;1)
а)  б)
б) 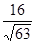 в)
в) 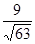 г)
г) 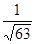
10. Укажите общий вид уравнения плоскости:
а) ax +by +d =0 б)ax +by +cz +d=0 в) ax +by =0 г) ax +d =0 .
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|