
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Рабочий лист.
Рабочий лист.
| Предмет | Математика |
| Группа | № 5 2 курс |
| Тема урока | Уравнение плоскости, сферы и прямой. |
| ФИО преподавателя | Тимиршина Алия Мунзиловна |
| Где находится задание: | |
| Учебник | М.И. Башмаков Математика, задачник, 2017г |
| Ссылка | http://www.belgtis.ru/images/obuch/pm/MatematikaZadachnikBashmakov.pdf |
| Сроки выполнения задания | 21.09.2020 до 17:00 |
| Как выполнять задание | Написать конспект и выполнить домашнее задание. |
| Домашняя работа | М.И. Башмаков Математика, задачник, 2017г , стр.106 № 5.30, стр.116 №5.54 |
| Обратная связь | Выполненные работы отправить личным сообщением ВК |
| Как узнать отметку о выполненном задании | Оценки будут выставлены в личный журнал преподавателя и отправлены в беседу ВК. |
Тема: Уравнение плоскости, сферы и прямой.
Выведем уравнение плоскости, проходящей через точку  и перпендикулярной вектору
и перпендикулярной вектору 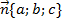 . (См. Рис. 1.)
. (См. Рис. 1.)
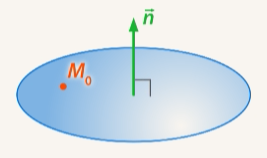
Рис. 1. Исходные данные
Оказывается, этого достаточно, чтобы задать плоскость. Действительно, раз вектор перпендикулярен плоскости, это равносильно тому, что он перпендикулярен двум пересекающимся прямым данной плоскости. Если рассмотреть такие две прямые, проходящие через точку 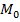 , они однозначно задают плоскость по следствию из аксиомы.
, они однозначно задают плоскость по следствию из аксиомы.
Как задать уравнение плоскости? Вообще, что такое уравнение плоскости? Уравнение плоскости – это уравнение, которому удовлетворяют координаты всех точек этой плоскости и только они.
Пусть 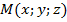 – произвольная точка пространства, отличная от
– произвольная точка пространства, отличная от 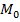 . Эта точка лежит в нашей плоскости тогда и только тогда, когда векторы
. Эта точка лежит в нашей плоскости тогда и только тогда, когда векторы  и
и 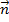 перпендикулярны. А это в свою очередь означает, что скалярное произведение этих векторов равно нулю. (См. Рис. 2.)
перпендикулярны. А это в свою очередь означает, что скалярное произведение этих векторов равно нулю. (См. Рис. 2.)
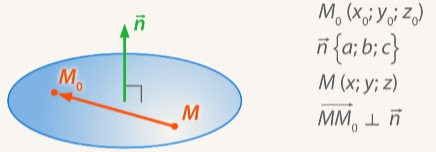
Рис. 2. 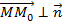
Запишем координаты вектора  :
: 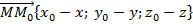 . Тогда скалярное произведение
. Тогда скалярное произведение 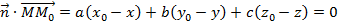 . Домножим всё на
. Домножим всё на 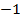 и раскроем скобки. Получим:
и раскроем скобки. Получим:
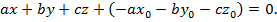
Обозначая  через
через 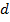 , приходим к общему (стандартному) виду уравнения плоскости:
, приходим к общему (стандартному) виду уравнения плоскости:
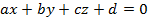
Обратите внимание, что для каждой плоскости существует такой набор коэффициентов 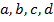 (и он не один, с точностью до домножения на число), который задает ее уравнение (а значит, и саму плоскость). Кстати, верно и обратное утверждение: любое уравнение такого вида задает плоскость. Действительно, по первым трем коэффициентам можно однозначно определить вектор, перпендикулярный плоскости, а коэффициент
(и он не один, с точностью до домножения на число), который задает ее уравнение (а значит, и саму плоскость). Кстати, верно и обратное утверждение: любое уравнение такого вида задает плоскость. Действительно, по первым трем коэффициентам можно однозначно определить вектор, перпендикулярный плоскости, а коэффициент 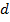 помогает установить необходимую точку из плоскости.
помогает установить необходимую точку из плоскости.
Уравнение плоскости в пространстве напоминает уравнение прямой на плоскости – только добавилась еще одна переменная (из-за трёхмерности пространства). Обратите внимание, что в данном уравнении 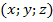 – координаты произвольной точки пространства и уравнение обращается в верное равенство тогда и только тогда, когда точка
– координаты произвольной точки пространства и уравнение обращается в верное равенство тогда и только тогда, когда точка 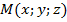 лежит в плоскости
лежит в плоскости 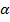 .
.
Также отметим, что коэффициенты при переменных в данном равенстве – это просто координаты вектора, перпендикулярного нашей плоскости. И это полезно запомнить: теперь, зная координаты вектора, перпендикулярного плоскости, и одной точки, лежащей в плоскости, мы легко можем построить ее уравнение.
Но верно и обратное утверждение: если дано уравнение плоскости, то легко можно выписать координаты вектора, ей перпендикулярного. Кстати, такой вектор называют нормальным или вектором нормали к плоскости.
Но ведь таких векторов бесконечно много. Конечно, но и уравнений плоскости бесконечно много – мы же можем домножить его на любую константу. Это и позволит получить любой нормальный вектор, коллинеарный исходному.
Примеры
Пример 1. Дан единичный куб 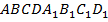 . Написать уравнение плоскости, проходящей через точку
. Написать уравнение плоскости, проходящей через точку 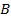 перпендикулярно прямой
перпендикулярно прямой 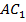 . Система координат задана. (См. Рис. 3.)
. Система координат задана. (См. Рис. 3.)
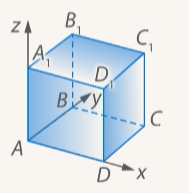
Рис. 3. Иллюстрация к задаче
Решение:
Найдем координаты интересующих нас вершин: 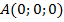 ,
, 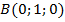 ,
, 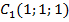 .
.
Значит, 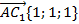 . Стандартное уравнение плоскости имеет вид:
. Стандартное уравнение плоскости имеет вид: 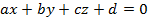 . Но ведь коэффициенты при переменных в данном равенстве – это просто координаты вектора, перпендикулярного нашей плоскости, то есть координаты вектора
. Но ведь коэффициенты при переменных в данном равенстве – это просто координаты вектора, перпендикулярного нашей плоскости, то есть координаты вектора 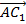 .
.
Таким образом, уравнение плоскости имеет вид 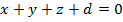 .
.
Мы знаем, что эта плоскость проходит через точку 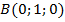 . Подставляя эти координаты в найденное уравнение плоскости, мы можем найти
. Подставляя эти координаты в найденное уравнение плоскости, мы можем найти 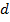 . Имеем:
. Имеем:
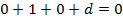
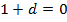

Получаем, что уравнение плоскости имеет вид 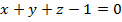 .
.
Ответ: 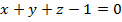 .
.
Пример 2. Пусть даны точки 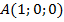 ,
, 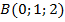 ,
, 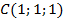 . Написать уравнение плоскости
. Написать уравнение плоскости 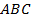 .
.
Решение:
Будем искать уравнение плоскости в виде 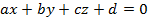 .
.
Подставив координаты точек 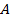 ,
, 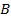 и
и 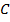 в уравнение, имеем систему:
в уравнение, имеем систему:
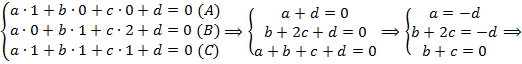
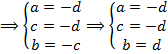
Итого, имеем: 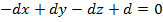 . Поделив на
. Поделив на 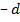 , имеем ответ:
, имеем ответ:
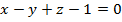
Ответ: 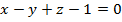 .
.
Заодно мы нашли координаты нормального вектора: 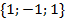 .
.
Домашнее задание: М.И. Башмаков Математика, задачник, 2017г , стр.106 № 5.30, стр.116 №5.54
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|