
Главная
Контакты
Случайная статья
|
Повторяем 6 класс и переходим к решению уравнений.
Повторяем 6 класс и переходим к решению уравнений.
| Что же значит решить линейное уравнение? Решить линейное уравнение — значит найти все те значения переменной, при каждом из которых это уравнение превращается в верное числовое равенство. Каждое такое значение переменной называется корнем уравнения. Запомните, что линейное уравнение с одной переменной всегда имеет только один корень (кроме одного случая)!
|
| |
|
Решение линейных уравнений
|
| Правило
|
Примеры
|
| –5х–150=0
| 15(х+2)–19=12х
| 6(1+5х)=5(1+6х)
| 15(х+2)–19=15х+21
|
| 1. Если нужно, раскрыть скобки.
| ––––––––––––
|
15(х+2)–19=12х
15х+15.2–19=12х
15х+30–19=12х
|
6(1+5х)=5(1+6х)
6.1+6.5х=5.1+5.6х
6+30х=5+30х
|
15(х+2)–19=15х+21
15х+15.2–19=15х+21
15х+30–19=15х+21
|
| 2. Перенести слагаемые с переменной в левую, а без переменной в правую часть уравнения, меняя их знаки на противоположные
(+ на – , а – на +)
|
–5х–150=0
–5х=150
|
15х+30–19=12х
15х–12х= –30+19
|
6+30х=5+30х
30х–30х=5–6
|
15х+30–19=15х+21
15х–15х= –30+19+21
|
| 3. Привести в обеих частях уравнения подобные слагаемые.
Получится уравнение вида ax=b
|
––––––––––––
| (15–12)х=–30+19
3х= –21
| (30–30)х=5–6
0х= –1
| 0х= 0
|
4. Если а¹0, то 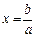 (x=b:a)
Если a=0, b¹0, то уравнение не имеет корней
Если a=0, b=0, то уравнение имеет бесконечное множество корней, т.е. х может принимать любые значения (x=b:a)
Если a=0, b¹0, то уравнение не имеет корней
Если a=0, b=0, то уравнение имеет бесконечное множество корней, т.е. х может принимать любые значения
| а= –5
x=150:(–5)
x= –30
Ответ: х= –30
| а=3
x= –21:3
x= –7
Ответ: х= –7
| а=0
решений нет
Ответ: решений нет
| x- любое число
Ответ: x- любое число
|
| | | | | | |
|
ТРЕНАЖЕР. РЕШЕНИЕ УРАВНЕНИЙ. АЛГЕБРА 7 КЛАСС
|
|
| 7 – 2х = 9 – 3х
| 11х = 6 + 5(2х – 1)
| 6(2х – 3) – 3х = 2х – 4
| 4(3х + 5) – 5(4х – 3) = 3
| 5х – 3(4х – 1) = 7 – 2(7х + 2)
| –5,6(x – 3) + 2,lx = –3,5x + 10
|
|
| 7х + 10 = 5х + 2
| 4(3х – 2) + 5 = 9
| 2х – 5 = 7(3х + 4) + 5
| 28 – 4(3х + 2) = 5(2х – 7)
| 3х – 4(5х + 2) – 6(3х – 4) = 1
| 7(x – 4) + 3 = 3(2x – 7) + x – 8
|
|
|
|
|
|
|
|
|
|
| 5 – 6х = –10х – 3
| 6(2х + 5) – 8х = 2
| 3 + 4(5х – 3) = 4х + 7
| 3(5х – 7) – 7(4х + 5) = х
| 2(6х – 5) – 7(3х – 5) = 4х – 1
| –12x + 4(x – 3) = – 8x – 12
|
|
| 17 – 2х = 5 – 6х
| 2(4х – 5) = 2х + 8
| 3х – 10 = 5х + 2(4х + 5)
| 6х – 6(2х + 5) = 4(5х – 1)
| 11 – 4(3х – 1) – 5(4х – 3) = 3х
| 8(x – 3) + 1 = 5(2x + 3) – 2х
|
|
|
|
|
|
|
|
|
|
| 9х + 13= 7х + 5
| 3(2х + 5) + 6 = 3
| 5х + 18 = 7х + 6(3х – 7)
| 3х – 7(3х – 4) = 5(2х – 7)
| 13 – 3(5х + 1) – 6(4х – 3) = 5х
| 4(x + 2) – 0,7 = 2(2x + 4) + 0,3
|
|
| –5х – 9 = –6х – 10
| 4х = 7 + 3(4х + 3)
| 5(3х + 1) + 2х = 4х + 5
| 3(7х – 1) – 6(5х + 2) = 3
| 3х – 5(2х + 3) = 15 – 4(6х – 1)
| 1,9x + 0,3(7 – x) = 2,1 – 0,2х
|
|
| 12х – 5 = 7х + 10
| 4(3х + 5) – 6х = 2
| 3х – 7 = 4(2х – 3) – 5
| 17 – 2(6х – 5) = 4(7х – 2)
| 6х – 3(5х + 4) – 2(7х – 3) = –6
| –2(x + 21) – 3(x – 14) = –5x
|
|
| 6х – 11 = х + 14
| 5(6х – 1) = 3х – 5
| 5 + 3(7х + 4) = 6х – 13
| 5(3х + 4) – 6(3х – 7) = 23х
| 4(5х – 3) – 5(3х + 7) = 6х – 23
| 2(x + 21) + 3(x – 4) = 5(x + 6)
|
|
| 10х + 15 = 7х + 6
| 3(4х – 1) + 5х = 14
| 4х + 8 = 6х + 4(5х + 2)
| 7(2х – 5) – 5(4х + 3) = 4х
| 8 – 7(2 – 5х) – 4(2х + 3) = 3х
| 2,1(x – 0,3) + 0,7x = 2,8x + 0,7
|
|
| 8х + 11 = 6х + 13
| 4(5х + 2) = 7х – 5
| 7(2х – 1) – 3х = х – 17
| 5х – 5(4х + 3) = 6(5х – 1)
| 4х – 7(3х – 5) = 4 – 3(4х – 7)
| 2,4(x – 0,1) – 0,26 = 2,4x – 0,4
|
|
| –4х – 21 = –7х – 3
| 7(3х – 4) – 5 = 9
| 5х + 4 = 3(6х + 5) + 2
| 6(2х + 3) – 2(7х – 4) = 23
| 7х – 5(4х – 5) – 2(6х + 7) = 1
| –11(x – 2) + (2x – 3) = –9x + 19
|
|
| 4 – 3х = –7х – 4
| 7х = 5 + 2(6х – 5)
| 9 + 5(4х – 3) = 7х – 6
| 25 – 4(3х + 5) = 7(4х + 3)
| 6(2х + 7) – 2(6х – 5) = 3х – 2
| 11(x – 2) – (2x – 3) = 9(x + 2)
|
|
| –3х – 10 = –12 – 5х
| 16х = 7(3х – 1) + 2
| 4 + 6(3х + 1) = 5х + 10
| 7(3х – 4) – 4(6х + 5) = –55
| 18 – 6(3х + 7) – 2(4х – 1) = 7х
| –1,7(x + 2) – 0,3x = 2(2 – x)
|
|
| 5 – 4х = 7 – 5х
| 6(2х – 3) + 4 = 10
| 7х – 4 = 4(2х – 7) + 2х
| 2 – 5(4х – 7) = 3(6х + 5)
| 3х – 6(5х + 2) = 4 – 5(3х + 4)
| –11(x – 2) + 2(3 – 2x) + 15x = 0
|
|
| 13 – 4х = 1 – 8х
| 5(3х + 4) – 2х = 7
| 3х – 10 = 4х + 3(5х + 2)
| 6(4х + 7) – 3(8х – 3) = 17х
| 4х – 3(6х – 1) – 7(4х – 3) = 10
| 2(x – 23) + 3(15 – x) = –(x + 1)
|
|
| –6х – 23 = –9х – 5
| 2(4х – 3) = 5х + 3
| 6х + 7 = 5(4х – 1) – 16
| 15х – 4(3х + 5) = 7(2х + 5)
| 5(3х – 8) – 3(2 – 5х) = 4х – 20
| 2(x – 23) + 3(15 – x) = –x + 1
|
|
| 7х + 10 = 5х + 12
| 3(2х – 5) + 5х = 7
| 5х – 3 = 6(2х + 5) + 2
| 17х – 3(5х – 4) = 8(3х – 4)
| 7(4х + 5) – 4(2 + 3х) = 6х – 3
| 2,1(2 – x) + 1,4(1,5x – 3) = 0
|
|
| 9х + 13= 6х + 4
| 9х = 3 + 4(5х + 2)
| 6 + 7(4х – 3) = 3х – 65
| 5(4х + 3) – 7(4х – 7) = 24
| 1 – 5(2х – 5) – 3(2 – 3х) = 4х
| 2,1(2 – x) + 1,4(1,5x – 3) = 2
|
|
| 9х – 7 = 4х + 18
| 7(3х + 1) = 4х – 10
| 6х + 14 = 4х + 5(3х + 8)
| 9 – 6(3х – 4) = 5(4х – 1)
| 2х – 4(5х – 3) = 21 – 7(3х + 2)
| 2,1(2x – 1) = 1,4(3x – 4) + 0,3
|
|
| 13х – 2 = 8х + 13
| 5(4х + 7) – 3 = 12
| 4(3х – 2) – 2х = 5х + 12
| 2(8х – 3) – 4(6х + 5) = 6х
| 5х – 2(7х + 2) – 3(4х + 5) = 2
| 21(x – 3) + 20 = 7(3x – 2)
|
|
| 11х – 3= 6х + 12
| 6(2х – 5) – 4 = 2
| 6х – 1 = 3х + 5(4х – 7)
| 4(6х + 5) – 5(7х – 4) = х
| 4х – 6(3х + 8) – 5(2х – 7) = 35
| 7(2x – 3) + 1 = 2(7x – 10)
|
|
| 7х – 8 = 2х + 17
| 2х = 3(2х + 1) + 5
| 7(2х + 3) + х = 4х – 12
| 7х – 3(4х – 3) = 7(3х + 5)
| 5(2 – 5х) – 7(4х – 1) = 6х – 42
| 2(8x – 1) – 8(2x – 3) = 13
|

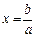 (x=b:a)
Если a=0, b¹0, то уравнение не имеет корней
Если a=0, b=0, то уравнение имеет бесконечное множество корней, т.е. х может принимать любые значения
(x=b:a)
Если a=0, b¹0, то уравнение не имеет корней
Если a=0, b=0, то уравнение имеет бесконечное множество корней, т.е. х может принимать любые значения