Метод интегрирования по частям

65-68

Свойства неопределенного интеграла, таблица интегралоd

Свойства:

1. 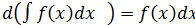дифференциал от неопределенного интеграла равен подинтегральному выражению

2. 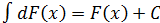неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной

3. 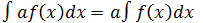постоянный множитель может быть вынесен за знак неопределенного интеграла

4. 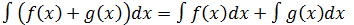неопределенный интеграл суммы функций равен сумме интегралов

5. Инвариантность формулы интегрирования
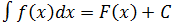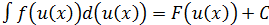Если , то , где 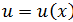- произвольная функция, имеющая непрерывную производную на (a;b)

Таблица интегралов:

66 Метод интегрирования по частям

Пусть 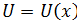и 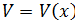непрерывны и дифференцируемые на (a;b)

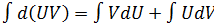
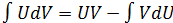
67 Интегрирование рациональных дробей, дробно-рациональная функция

Неопределенный интеграл от любой рациональной дроби на всяком (a;b), где знаменатель не равен нулю, существует и выражается через элементарные функции, представляющие собой линейную комбинацию рациональных дробей, логарифмов, arctg.

68) Интегрирование простейших иррациональных дробей, интегралы от дифференциальных биномов