
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Методические указания к решению задач по теме «Матрицы».
Методические указания к решению задач по теме «Матрицы».
Задание 1.Дана функция 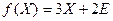 , где переменная
, где переменная 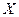 является матрицей соответствующего порядка,
является матрицей соответствующего порядка, 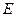 есть единичная матрица того же порядка. Найти
есть единичная матрица того же порядка. Найти 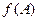 , если
, если 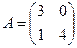 .
.
Решение. Подставим в функцию вместо матрицы 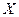 матрицу
матрицу 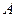 , а также единичную матрицу
, а также единичную матрицу 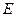 второго порядка.Выполняя действия умножения матрицы на число и сложения матриц, получим:
второго порядка.Выполняя действия умножения матрицы на число и сложения матриц, получим:
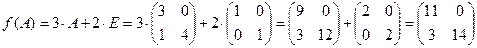 . ■
. ■
Задание 2.Решить матричное уравнение: 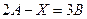 , если
, если 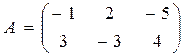 и
и 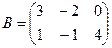 .
.
Решение. Выразим матрицу 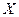 из уравнения, выполним операции умножения матриц на число и найдем разность матриц:
из уравнения, выполним операции умножения матриц на число и найдем разность матриц:
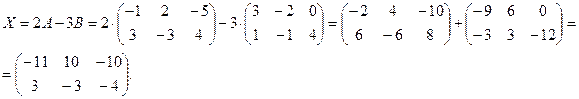 ■
■
Задание 3.Найти 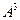 , если
, если 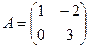 .
.
Решение. Найдем квадрат матрицы 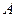 , умножая матрицу
, умножая матрицу 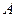 на себя, получим:
на себя, получим:
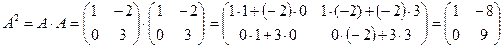 . Аналогично рассуждая, будем иметь:
. Аналогично рассуждая, будем иметь:
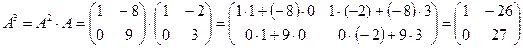 . ■
. ■
Задание 4.Выполнить действия над заданными матрицами:
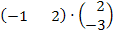
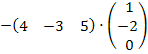 .
.
Решение.
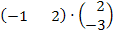
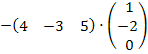 =
= 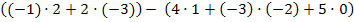 =
= 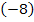 +
+ 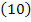 =
= 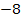 +10 = 2. Здесь матрица 1-го порядка отождествляется с ее элементом. ■
+10 = 2. Здесь матрица 1-го порядка отождествляется с ее элементом. ■
Задание 5.Дана матрица 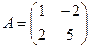 . Найти
. Найти 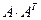 и
и 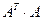 .
.
Решение.
Транспонируем матрицу 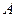 , заменяя все строки столбцами с теми же номерами:
, заменяя все строки столбцами с теми же номерами:
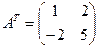 . Найдем произведение матриц:
. Найдем произведение матриц:
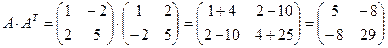 ;
;
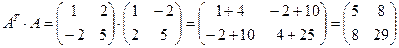 .
.
Очевидно, что 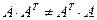 . Следовательно, матрицы
. Следовательно, матрицы 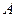 и
и 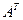 не являются перестановочными. ■
не являются перестановочными. ■
Задание 6.Привести к каноническому виду матрицу 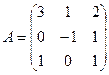 .
.
Решение. Применяя элементарные преобразования к строкам и столбцам матрицы, получим:
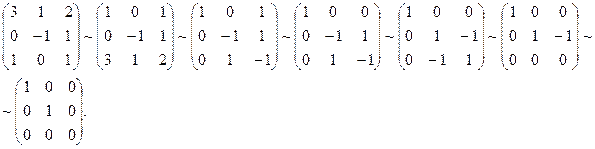 ■
■
Здесь мы произвели элементарные преобразования строк и столбцов матрицы в следующей последовательности:
o переставили 1-ю и 3-ю строки;
o прибавили к элементам 3-ей строки соответствующие элементы 1-ой строки, умноженные на (–3);
o прибавили к элементам 3-го столбца соответствующие элементы 1-го столбца, умноженные на (–1);
o переставили 2-ю и 3-ю строки;
o прибавили к 3-ей строке 2-ю;
o прибавили к 3-му столбцу 2-ой. ■
Задание 7.Даны три матрицы 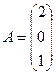 ,
, 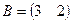 ,
, 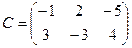 . Определить, в какой последовательности можно перемножить данные матрицы. Найти это произведение матриц.
. Определить, в какой последовательности можно перемножить данные матрицы. Найти это произведение матриц.
Решение. Известно, что число столбцов первой из перемножаемых матриц должно быть равно числу строк второй матрицы. Поэтому нельзя найти 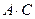 и
и 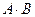 . Найдем произведение матрицы
. Найдем произведение матрицы 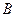 размерности
размерности 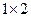 на матрицу
на матрицу 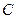 размерности
размерности 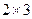 . В результате мы получим матрицу размерности
. В результате мы получим матрицу размерности 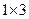 , которую можно умножить на матрицу
, которую можно умножить на матрицу 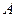 размерности
размерности 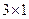 . Итоговая матрица будет иметь размерность
. Итоговая матрица будет иметь размерность 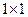 , т.е. отождествляется с числом.
, т.е. отождествляется с числом.
Таким образом, будем иметь:
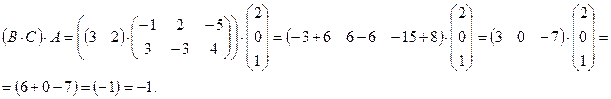 ■
■
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|