Практическая работа №1. Задания

Практическая работа №1

Решение задач оптимизации функций одной переменной

Задания

Найти экстремумы следующих функций:

1.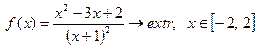
2.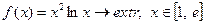
3.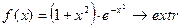
4.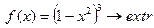
5.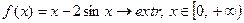

В задачах 3 и 4 рассмотреть функцию на всей числовой прямой. Задачу 4 решить с использованием второй и третьей производных.

При решении задач нужно руководствоваться следующим алгоритмом:

1. Найти ОДЗ функции и учитывать ее при решении задачи.

2. Найти стационарные точки и исследовать поведение функции в окрестности каждой такой точки. Для этого во всех задачах, кроме пятой, можно использовать первую производную, проанализировав изменение знака при переходе через точку, или производные более высоких порядков.

3. Найти точки разрыва функции и производной. Исследовать поведение функции в окрестности каждой точки разрыва. Для этого найти пределы функции слева и справа.

4. Исследовать поведение функции на границах. Для задач безусловной оптимизации найти пределы функции при x®+¥ и x®-¥. Для задач условной оптимизации найти значение функции на границе.

5. Из всех рассмотренных точек выбрать точки с наибольшими и наименьшими значениями.

Решить задачу оптимизации – это указать точку, в которой достигается наименьшее (наибольшее) значение и значение функции в этой точке. Если это невозможно, тогда:

1. найти sup или inf (точную верхнюю или нижнюю грань функции);

2. показать, что функция не является ограниченной снизу или сверху.