
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задания для практической работы.
Практическое занятие № 4
Тема: «Решение систем линейных уравнений методом Гаусса»
Цели:
· закрепить и систематизировать теоретические знания,
· формировать умения и навыки решения практических задач по теме.
В результате выполнения работы студент должен знатьосновные понятия.
Должен уметьвычислять определители.
План выполнения практической работы
1. Изучение методических рекомендаций по выполнению упражнений и решению задач.
2. Выполнение практической самостоятельной работы по вариантам.
3. Письменные ответы на контрольные вопросы
Задания для практической работы.
1. Изучение методических рекомендаций по выполнению упражнений и решению задач.
Метод Гаусса
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Правило Крамера непригодно в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу!.
Решим систему линейных уравнений методом Гаусса
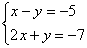 На первом этапе нужно записать расширенную матрицу системы:
На первом этапе нужно записать расширенную матрицу системы:
Расширенная матрица системы – это матрица системы плюс столбец свободных членов, в данном случае: 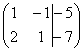 . Любую из матриц можно для краткости называть просто матрицей.
. Любую из матриц можно для краткости называть просто матрицей.
Умножаем первую строку на –2: и ко второй строке прибавляем первую строку умноженную на –2:
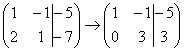 Делим вторую строку на 3. В результате элементарных преобразований получена эквивалентная исходной система уравнений:
Делим вторую строку на 3. В результате элементарных преобразований получена эквивалентная исходной система уравнений: 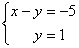
Рассмотрим первое уравнение системы 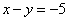 и подставим в него уже известное значение «игрек»:
и подставим в него уже известное значение «игрек»: 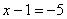
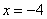 Ответ:
Ответ: 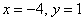
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|