
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПЕРЕВОД ЧИСЛА ИЗ ЛЮБОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДЕСЯТИЧНУЮ
ПЕРЕВОД ЧИСЛА ИЗ ЛЮБОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДЕСЯТИЧНУЮ
Чтобы перевести, например, 10045N, из системы счисления с основанием N в десятичную систему, нужно умножить значение каждой цифры на N в степени, равной разряду этой цифры:

ОСОБЕННОСТИ ПРИ ПЕРЕВОДАХ В РАЗНЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Некоторые правила, которые нужно знать, при работе с системами счисления:
· последняя цифра (крайняя справа) в записи числа в системе счисления с основанием N – представляет собой остаток от деления этого числа на N:
710 = 1112
7/2 = остаток 1
· две крайние справа цифры числа в системе счисления с основанием N – это остаток от деления этого числа на N², и так далее:
710 = 1112
112=310
7/22 = остаток 310 (112)
· десятичное число 10N записывается как единица и N нулей:

o тогда как десятичное число 2N в двоичной системе записывается как единица и N нулей:
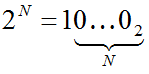
o а десятичное число 3N записывается в троичной системе в виде единицы и N нулей:
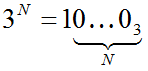
o можно сделать аналогичные выводы для любой системы счисления с основанием a; общее правило:
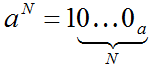
o десятичное 10N-1 записывается как N девяток:

o тогда как десятичное число 2N-1 в двоичной системе записывается как N единиц:
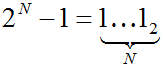
o а десятичное число 3N-1 записывается в троичной системе как N двоек:
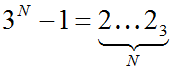
o значит есть общее правило: число aN-1 в системе счисления с основанием aзаписывается как N старших цифр этой системы, то есть, цифр (a-1)
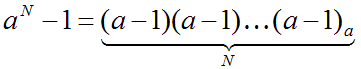
o десятичное число 10N-10M = 10M * (10N-M – 1) записывается как N-M девяток, за которыми стоят M нулей:
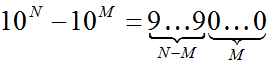
o тогда как десятичное число 2N – 2K при K < N в двоичной системе записывается как N – K единиц и K нулей:
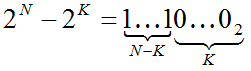
o то есть, существует общее правило:
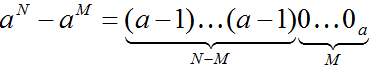
o Также следует знать, что верны равенства:
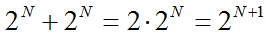

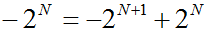
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|