Свойства модуля. Простейшее уравнение с модулем. Геометрический смысл модуля. Пример 1.

Определение. Абсолютной величиной (модулем) действительного числа a называют неотрицательное число | a | , которое определяется по формуле:

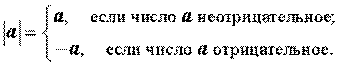
Так, например,| 5 | = 5, | – 2 | = 2, | 0 | = 0.

Свойства модуля

Если x и y – действительные числа, то справедливы равенства:

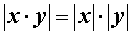
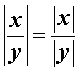
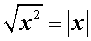
Кроме того, справедливо соотношение:

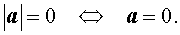
В то же время справедливы неравенства:

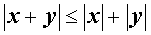	(неравенство треугольника)

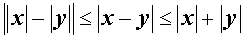
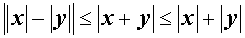
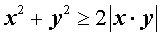
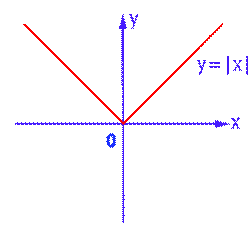
График функции y = | x |

График функции y = | x | имеет следующий вид:

Простейшее уравнение с модулем

Рассмотрим простейшее уравнение с модулем, имеющее вид:

| f (x) | = g(x) .

Поскольку

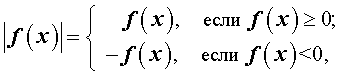
то данное уравнение эквивалентно совокупности двух систем:

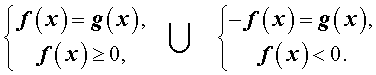
Для решения исходного уравнения остается лишь решить две этих системы и объединить полученные ответы.

Геометрический смысл модуля

Модуль числа — это расстояние от нуля до данного числа.

Например, |-5| = 5. То есть расстояние от точки -5 до нуля равно 5.

Рассмотрим простейшее уравнение |x| = 3. Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно трём. Это точки 3 и -3. Значит, у уравнения |x| = 3 есть два решения: x = 3 и x = -3.

Пример 1.

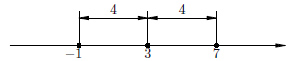
|x — 3| = 4.

Это уравнение можно прочитать так: расстояние от точки 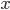до точки 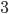равно 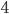. С помощью графического метода можно определить, что уравнение имеет два решения: 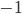и .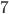

Пример 2.

Решим неравенство: |x + 7| < 4.

Можно прочитать как: расстояние от точки 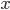до точки 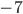меньше четырёх. Ответ: (-11; -3).