Контакты

Случайная статья

Корни натуральной степени и их свойства

Корни натуральной степени и их свойства

Арифметическим корнем n-ой степени из неотрицательного числа 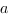называется неотрицательное число, n-я степень которого равна :

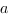Степень корня – это натуральное число, большее 1.

, ,

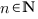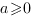
2.

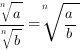
3.

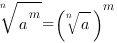
4.

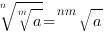
5.

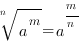
Частные случаи:

1. Если показатель корня целое нечетное число ( 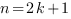), то подкоренное выражение может быть отрицательным.

В случае нечетного показателя уравнение 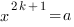при любом действительном значении 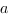и целом 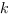ВСЕГДА имеет единственный корень:

,

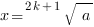Для корня нечетной степени справедливо тождество:

,

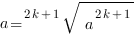2. Если показатель корня целое четное число ( ), то подкоренное выражение не может быть отрицательным.

В случае четного показателя уравнение 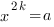имеет

при 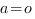единственный корнь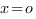

и, если и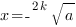

Для корня четной степени справедливо тождество:

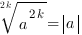
Для корня четной степени справедливы равенства:

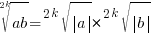
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.