
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая значимость закона Харди – Вайнберга
Ознакомитесь с видеоматериалом по ссылке https://www.youtube.com/watch?v=TSzb5zDZ9Co и материалом, представленным ниже. Составьте конспект урока и ответьте на вопросы письменно. Выполненное задание сфотографируйте и пришлите в ВК
Генетические процессы в популяциях
Генотипы особей одной популяции сходны, но все же не идентичны. Наибольший интерес представляет собой наличие в популяции тех или иных аллелей генов.
Гены, для которых имеются несколько аллелей, называются полиморфными (схема 1).

Схема 1. Аллели – разные формы гена А: А, А* и А**
Для одного и того же гена набор аллелей в разных популяциях может отличаться.
Кроме того, одни и те же аллели могут быть распределены среди особей по-разному, т. е. быть в гомо- или гетерозиготном состоянии. Количество аллелей и количество типов распределения аллелей определяет генетическое разнообразие популяции.
От уровня генетического разнообразия зависит интенсивность эволюционных процессов и стабильность генотипа популяции.
Количество аллелей и соотношение гомо- и гетерозигот определяет генетическое разнообразие популяции.
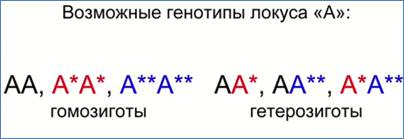
Схема 2. Разные варианты комбинации трех аллелей гена А.
От уровня генетического разнообразия зависит интенсивность эволюционных процессов.
Закономерности генетических процессов в популяции можно изучать только при условии свободного скрещивания. Т. е. такого скрещивания, при котором вероятность соединения любых гамет и комбинации их признаков одинакова.
Изучая генетические процессы в естественных популяциях, английский ученый Пирсон (рис. 1) в 1904 году вывел закон стабилизирующего скрещивания, или закон Пирсона.

Рис. 1. Пирсон
Он может быть сформулирован так: при любом исходном соотношении частот гомозигот и гетерозигот при первом скрещивании внутри популяции устанавливается состояние равновесия, если исходные частоты аллелей одинаковы у обоих полов.
Конкретный вид этого равновесия можно описать с помощью элементарной математической формулы, которую независимо вывели английский математик Дж. Харди и немецкий врач и биолог В. Вайнберг (рис. 2).

Рис. 2. Дж. Харди и В. Вайнберг
Закон Харди – Вайнберга гласит, что частота гомозиготных и гетерозиготных организмов в условия свободного скрещивания при отсутствии давления отбора и других факторов пребывает в состоянии равновесия.
В простейшем виде закон описывается следующей формулой (схема 3):

Схема 3. Закон Харди – Вайнберга
Практическая значимость закона Харди – Вайнберга
Расчёт частот аллелей, по закону Харди – Вайнберга, имеет большое значение для медицины. Медики рассчитывают частоту возникновения генетических заболеваний. Величина человеческой популяции достаточно велика, чтобы можно было опираться на вычисления с помощью этого закона. Также этот закон используется селекционерами, для определения сроков закрепления нужных признаков.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|