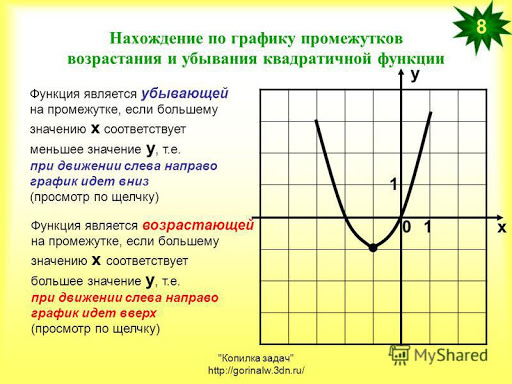
Возрастание и убывание функции.

Возрастание и убывание функции.

Теоретический материал для самостоятельного изучения

1. Функция y = f(x), определенная на промежутке Х, называется возрастающей на этом промежутке, если для любой пары чисел х₁ и х₂ из этого промежутка из неравенства х₁< х₂следует неравенство f(x₁) <f(x₂)

2. Функция y = f(x), определенная на промежутке Х, называется убывающей на этом промежутке, если для любой пары чисел х₁ и х₂ из этого промежутка из неравенства х₁< х₂следует неравенство f(x₁) >f(x₂)

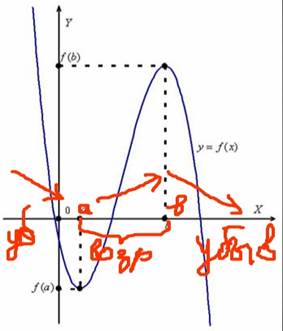
На промежутке (- 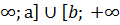) - функция убывает; а на промежутке (а;b) - функция возрастает.

Точка a- называется точкой минимума, b- точкой максимума.

Х_min=а; Х_max=b.

Точки минимума и точки максимума так же ещё называются точками экстремума.А значение функции в этих точках называются Экстремумами функции. На чертеже f(a)- минимум функции ( эстремум). f(b)- максимум функции (тоже экстремум)

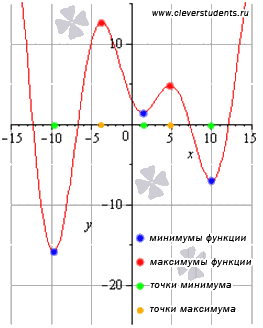
Пример: Найти промежутки возрастания и убывания и точки экстремума.

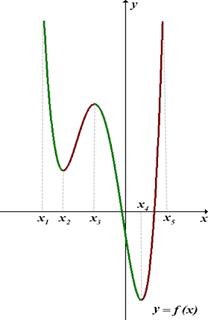
(х₁; х₂) 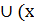_3;х₄)- функция убывает. (Зелёный участок графика)

(х₂; х₃) 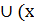_4;х₅)- функция возрастает (красный участок графика).

Точки экстремума:

Х_min₁=х₂; - точка минимума .

Х_min₂=х₄; - точка минимума

х_max=х₃; - точка максимума