
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Операции над графами
Основные понятия и определения теории графов
Графы используют как математические модели во многих научных и прикладных задачах. Широкое применение графов объясняется наглядностью построенной модели – обычно человек легко запоминает и различает особенности графических объектов. При этом графы встречаются в различных областях науки и техники под разными названиями: структуры данных – в вычислительной технике; сети – в электротехнике, в задачах управления транспортными потоками; социограммы – в экономике и социологии; молекулярные структуры – в химии.
Определение. Пусть задано множество Х = {х1,х2,…,хn} и бинарная операция Т, сопоставляющая каждому элементу xi 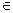 X множество {(xi,xj)|xi
X множество {(xi,xj)|xi 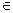 X, xj
X, xj 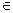 X }. Операцию Т можно представить как Т = Т(x1)
X }. Операцию Т можно представить как Т = Т(x1) 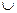 Т(x2)
Т(x2) 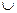 …
… 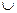 Т(xn), где Т(xi) – множество пар, у которых на первом месте стоит элемент xi. При этом элементы xi
Т(xn), где Т(xi) – множество пар, у которых на первом месте стоит элемент xi. При этом элементы xi 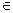 X будем называть вершинами, а пары (xi, xj) – дугами, если они упорядочены, и рѐбрами, если нет.
X будем называть вершинами, а пары (xi, xj) – дугами, если они упорядочены, и рѐбрами, если нет.
Говорят, что множество Х и бинарная операция Т задает граф Г(Х,Т) или Г и при этом:
- две вершины, определяющие ребро или дугу, называют смежными;
- два ребра, имеющие общую вершину, называют смежными;
- вершины, определяющие ребро (дугу), называют инцидентными этому ребру (дуге).
Граф, в котором операция Т задаѐт упорядоченные пары, называется ориентированным или орграфом. Отношения порядка в графе задаются стрелками.
Пример 1.
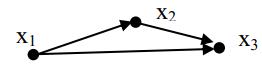
Описать математически данный орграф.
Решение
Х={х1,х2,х3}, T=Т(x1) 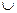 Т(x2)
Т(x2) 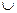 Т(x3), Т(x1)={(х1,х2),(х1,х3)}, Т(x2)={(х2,х3)}, Т(x3)=
Т(x3), Т(x1)={(х1,х2),(х1,х3)}, Т(x2)={(х2,х3)}, Т(x3)= 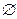 , T={(х1,х2),( х1,х3), (х2,х3)}.
, T={(х1,х2),( х1,х3), (х2,х3)}.
Ребро называется петлѐй, если оно заканчивается в одной и той же вершине.
Если хотя бы одну пару вершин графа Г соединяют несколько ребер, то такой граф называют мультиграфом.
Вершину графа Г называют изолированной, если она не инцидентна ни одной вершине этого графа.
Граф Г называется полным, если каждая пара его вершин соединена ребром. Если граф Г не имеет ребер, то такой граф называется нуль-графом.
Операции над графами
Пусть заданы два неориентированных графа Г1(Х1,Е1) и Г2(Х2,Е2).
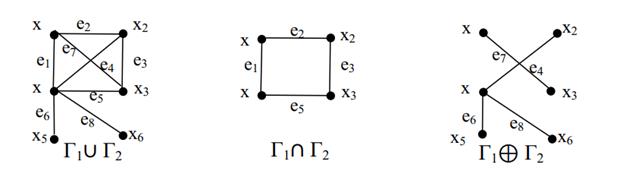
Определение. Объединением графов Г1(Х1,Е1) и Г2(Х2,Е2) называется граф Г3(Х3,Е3) (Г3= Г1 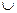 Г2), такой что Х3= Х1
Г2), такой что Х3= Х1 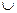 Х2,
Х2,
Е3=Е1 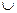 Е2.
Е2.
Определение. Пересечением графов Г1(Х1,Е1) и Г2(Х2,Е2) называется граф Г4(Х4,Е4) (Г4= Г1 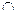 Г2), такой что Х4= Х1
Г2), такой что Х4= Х1 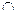 Х2, Е4=Е1
Х2, Е4=Е1  Е2.
Е2.
Определение.Граф Г5(Х5,Е5) называется кольцевой суммой графов Г1(Х1,Е1) и Г2(Х2,Е2) (Г5= Г1  Г2), если он представляет собой граф, не имеющий изолированных вершин и порожденный на множестве ребер Е5= Е1
Г2), если он представляет собой граф, не имеющий изолированных вершин и порожденный на множестве ребер Е5= Е1  Е2, то есть состоит только из ребер присутствующих в Г1 или в Г2, но не в обоих графах одновременно.
Е2, то есть состоит только из ребер присутствующих в Г1 или в Г2, но не в обоих графах одновременно.
Пример 2. Заданы графы Г1(Х1,Е1) и Г2(Х2,Е2).
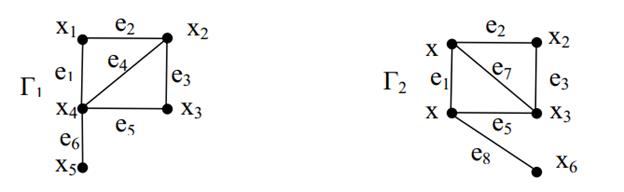
Построить: Г1  Г2, Г1
Г2, Г1  Г2, Г1
Г2, Г1  Г2.
Г2.
Решение
Определение. Граф 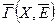 называется дополнением исходного графа Г(X,E), если ребро
называется дополнением исходного графа Г(X,E), если ребро 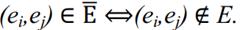
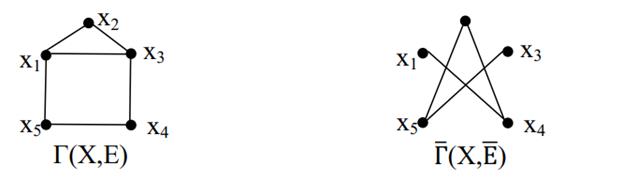
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|