
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Система линейных уравнений.. A|= -главный определитель системы. Решение системы линейных уравнений. Метод КРАМЕРА. Практическое задание.
Система линейных уравнений.
Общий вид системы:
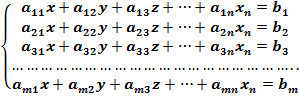
В матричном виде система имеет вид:
AX=B, где А= 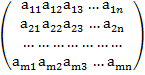 X=
X=  B=
B= 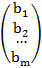
Система трех линейных уравнений с тремя неизвестными имеет вид:
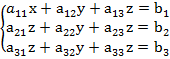
A= 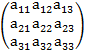 B=
B= 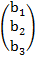 X=
X= 
Δ=|A|= -главный определитель системы
Δ 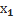 =
= 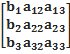 Δ
Δ  =
= 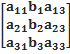 Δ
Δ 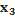 =
=  -
-
-вспомогательные определителисистемы
Решение системы линейных уравнений
Метод КРАМЕРА
Если главный определитель системыΔ ≠ 0, то система имеет единственное решение, которое находиться по формулам Крамера:
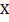 =
= 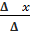 ; Y=
; Y= 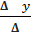 ;
; 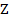 =
= 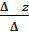
Если Δ =0 и Δxi≠ 0, то система не имеет решения.
Если 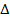 =0 и Δxi=0, то система имеет бесконечно много решений.
=0 и Δxi=0, то система имеет бесконечно много решений.
Пример:
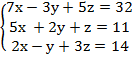
Находим:
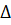 =
=  =7·
=7· 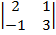 -(-3)
-(-3) 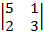 +5
+5 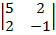 =
=
=7(6+1)+3(15-2)+5(-5-4)=49+39-45=43  ≠ 0
≠ 0
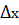 =
=  =32
=32 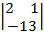 -(-3)
-(-3) 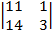 +5
+5 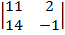 =
=
=32(6+1)+3(33-14)+5(-11-28)=32·7+3·19+5·(-39)=
=224+57-195=86
 =
= 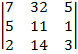 =7
=7  -32
-32 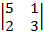 +5
+5 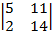 = -43
= -43
 =
= 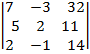 =7
=7 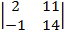 -(-3)
-(-3) 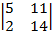 +32
+32 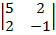 =129
=129
По формулам Крамера находим:
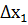 =
= 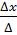 =
= 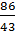 = 2;
= 2; 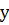 =
= 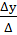 =
= 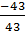 = -1;
= -1; 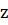 =
= 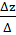 =
= 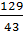 = 3
= 3
Ответ: (2;-1;3).
Практическое задание.
Решить систему методом Крамера.


|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|