
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа №3. Задания для практической работы.. Изучение методических рекомендаций по выполнению упражнений и решению задач.
Практическая работа №3
Тема: “Решение систем линейных уравнений матричным методом”
Знания: Определение равных матриц, находить произведение матриц;
находить обратную матрицу;
Умения: применять полученные знания для решения систем линейных уравнений матричным способом.
План выполнения практической работы
1. Изучение методических рекомендаций по выполнению упражнений и решению задач.
2. Выполнение практической самостоятельной работы по вариантам.
3. Письменные ответы на контрольные вопросы
Задания для практической работы.
1. Изучение методических рекомендаций по выполнению упражнений и решению задач.
Пусть дана система уравнений.
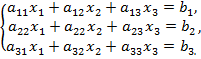
Рассмотрим матрицу, составленную их коэффициентов при неизвестных:
A= 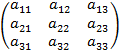
Свободные члены и неизвестные можно записать в виде матриц-столбцов:
B= 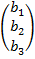 , X=
, X= 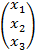 .
.
Тогда, используя правило умножения матриц, эту систему можно записать так:
 =
= 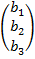 или A*X=B.
или A*X=B.
Это равенство называется простейшим матричным уравнением.
Такое уравнение решается следующим образом:
Пусть матрица А- невырожденная (D≠0); тогда существует обратная матрица 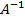 .
.
Умножив на неё обе части матричного уравнения, имеем:
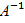 *(A*X)=
*(A*X)= 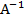 *B.
*B.
Используя сочетательный закон умножения перепишем это равенство в виде:
( 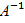 *А)*Х=
*А)*Х= 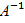 *В или Е*Х=
*В или Е*Х= 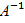 *В, следовательно Х=
*В, следовательно Х= 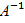 *В.
*В.
Пример.
Решить матричным способом систему уравнений
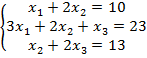
Решение.
Составим матричное уравнение
A*Х=B, где
A=  , X=
, X= 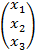 , B=
, B= 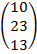
Находим
∆=  =4-12-1=-9≠0;
=4-12-1=-9≠0;
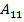 =3;
=3; 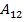 =-6;
=-6; 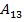 =3;
=3; 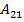 =-4;
=-4; 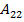 =2;
=2; 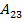 =-1;
=-1; 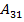 =2;
=2; 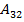 =-1;
=-1; 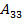 =-4;
=-4;
Составим матрицу 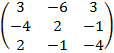 и транспонируем ее
и транспонируем ее 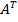 =
= 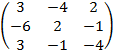
Запишем обратную матрицу:
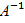 =
= 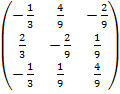
Следовательно, Х= 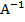 *В=
*В= 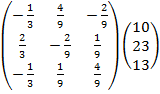 =
= 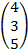
Итак, решение системы уравнений 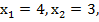
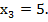
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|