Практическая работа №3. Название работы: Деление окружности на равные части

Практическая работа №3

Название работы: Деление окружности на равные части

Цель работы:приобретение практических навыков по технике выполнения чертежей и знанийв области геометрических построений.

Цель:Познакомиться с правилами деления окружностей на равные части и приобрести навыки выполнения делений окружности на части при вычерчивании детали, изделия.

Материалы и оборудование: бумага формата А4, простые карандаши, чертежные инструменты, готовальня, ластик.

Литература:

1. Ф. И. Пуйческу, С. Н. Муравьев, Н. А. Чванова. Инженерная графика. – М. Издательство «Академия», 2013,320с.

2. А. М. Бродский. Э. М. Фазлулин. В. А. Халдинов. Инженерная графика.- М. Издательство «Академия», 2010, 400с.

3. В. П. Покатаев, С. Д. Михеев. Дизайн и оборудование городской среды.Ростов н/Д. Феникс,2012, 408с.

Основные понятия:В практике при выполнении чертежей деталей встречаются случаи,гдетребуется деление окружности на равные части, которое выполняют с помощью треугольников, циркуля. Прежде чем приступить к выполнению задания, нужно изучить технику выполнения геометрических построений по методическому пособию и главы 5-6 в учебнике «Черчение» С.К. Боголюбов (стр.31-34).

1. Деление окружности на три равные части

Из конца диаметра, например, точки А (рис.1) проводят дугу радиусом R, равным радиусу заданной окружности. Получают первое и второе деление – точки 1 и 2. Третье деление точка 3, находится на противоположном конце того же диаметра. Соединив точки 1,2,3 хордами, получают правильный вписанный треугольник.

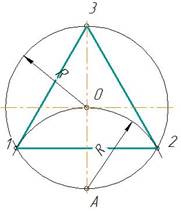
Рис. 1

2. Деление окружности на шесть равных частей

Из концов какого-либо диаметра, например АВ (рис.2), описывают дуги радиусом R окружности. Точки А, 1,3,В,4,2 делят окружность на шесть равных частей. Соединив их хордами, получают правильный вписанный шестиугольник.

Примечание. Вспомогательные дуги проводить полностью не следует, достаточно сделать засечки на окружности.

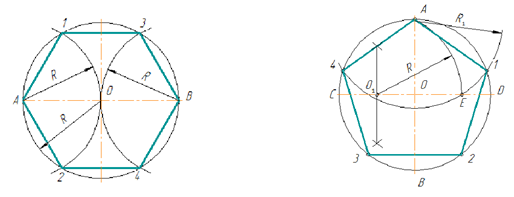
Рис. 2 Рис. 3

3. Деление окружности на пять равных частей

1. Проводят два взаимно перпендикулярных диаметра АВ и CD (рис.3). Радиус ОС в точке О₁ делят пополам.

2. Из точки О₁, как из центра, проводят дугу радиусом О₁А до пересечения ее с диаметром CD в точке Е.

3. Отрезок АЕ равен стороне правильного вписанного пятиугольника, а отрезок ОЕ –

стороне правильного вписанного десятиугольника.

4. Приняв точку А за центр, дугой радиуса R₁ = АЕ на окружности отмечают точки 1 и 4.

Из точек 1 и 4, как из центров, дугами того же радиуса R₁ отмечают точки

3 и 2.

Точки А,1,2,3,4 делят окружность на пять равных частей.

4. Деление окружности на семь равных частей

Из конца диаметра, например, точки А проводят дугу радиуса R, равного радиусу окружности (рис.6). Хорда CD равна стороне правильного вписанного треугольника. Половина хорды CD с достаточным приближением равняется стороне правильного вписанного семиугольника, т.е. делит окружность на семь равных частей.

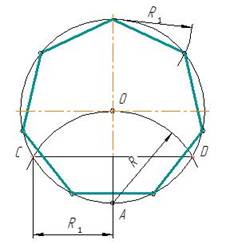
R₁ = CD/2

Рис. 6

Исходные данные (задание):Разделить окружность на три,пять равные части.

Порядок выполнения:

1. Провести центровые линии и построить 2 окружности диаметром 60мм.,

2. Разделить окружность на три части при помощи циркуля и треугольника.

3. Разделить окружность на пять частей при помощи циркуля.

Перечень оборудования: (ТСО, наглядные пособия):Образцы деталей с равномернорасположенными элементами по окружности.

Вопросы для повторения:

1. Как разделит окружность на 4 и 8частей?

2. Как разделить окружность на 3 и 6 частей?

3. Как разделить окружность на 5 и 10 частей?

4. Как разделить окружность на 7 частей?

Литература:

1. С.К. Боголюбов, Черчение. – М.: Машиностроение, 1989 стр. 35-39.

2. О.М. Букова, Е.В. Ларионова Техника черчения. Геометрические построения. Авторская педагогическая разработка, Иркутск, 2013. – 24с.:ил

3. Пример выполнения работы:Стенд с образцами работ