
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ
АВТОНОМНАЯ НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ
«КАЛИНИНГРАДСКИЙ бизнес колледж»
Ю. А. ЯПАРОВА
Методические указания
к практическим занятиям по курсу
«ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ»
Часть 1
Количественная оценка информации и энтропия
Калининград
2015
Автор: Ю.А. Япарова - преподаватель АНО «Калининградский бизнес колледж»
Япарова Ю.А. Методические указания к практическим занятиям по курсу «ТЕОРИЯ ИНФОРМАЦИИ», Часть 1 Количественная оценка информации и энтропия. – Для студентов специальности 230111 «Компьютерные сети».
Калининград: АНО «Калининградский бизнес колледж», 2015.- 13 с.
Методические указания содержат примеры решения задач по количественной оценке информации и вычислению энтропии. Данное пособие подходит как для самостоятельного изучения, так и для проведения занятий в рамках курса «Теория информации».
ФОРМУЛЫ, НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ
Общее число неповторяющихся сообщений, которое может быть составлено из алфавита мощности m путем комбинирования по n символов в сообщении,
N = mn.
Энтропия символа исходного алфавита, составленного из равновероятных и взаимонезависимых символов,
Н = log m.
Так как информация есть неопределенность, снимаемая при получении сообщения, то количество информации может быть представлено как произведение общего числа сообщений к на среднюю энтропию Н, приходящуюся на одно сообщение:
I = кН бит.
Для неравновероятных алфавитов энтропия на символ алфавита
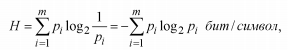
а количество информации в сообщении, составленном из к неравновероятных символов,
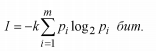
При решении задач, в которых энтропия вычисляется как сумма произведений вероятностей на их логарифм, вероятности всегда должны представлять группу полных событий, независимо от тога, являются ли они безусловными p(ai), условными p(a/bi) или вероятностями совместных событий р(ai,bi).
Для упрощения вычислений при решении задач ниже приведены таблица значений величин -p Log2p и таблица двоичных логарифмов целых чисел.
| p | -p Log2P | P | -p Log2P | P | -p Log2P |
| 0,01 | 0,0664 | 0,36 | 0,5306 | 0,71 | 0,3508 |
| 0,02 | 0,1129 | 0,37 | 0,5307 | 0,72 | 0,3412 |
| 0,03 | 0,1518 | 0,38 | 0,5305 | 0,73 | 0,3314 |
| 0,04 | 0,1858 | 0,39 | 0,5298 | 0,74 | 0,3215 |
| 0,05 | 0,2161 | 0,4 | 0,5288 | 0,75 | 0,3113 |
| 0,06 | 0,2435 | 0,41 | 0,5274 | 0,76 | 0,3009 |
| 0,07 | 0,2686 | 0,42 | 0,5256 | 0,77 | 0,2903 |
| 0,08 | 0,2915 | 0,43 | 0,5236 | 0,78 | 0,2796 |
| 0,09 | 0,3127 | 0,44 | 0,5211 | 0,79 | 0,2687 |
| 0,1 | 0,3322 | 0,45 | 0,5184 | 0,8 | 0,2575 |
| 0,11 | 0,3503 | 0,46 | 0,5153 | 0,81 | 0,2462 |
| 0,12 | 0,3671 | 0,47 | 0,5120 | 0,82 | 0,2348 |
| 0,13 | 0,3826 | 0,48 | 0,5083 | 0,83 | 0,2231 |
| 0,14 | 0,3971 | 0,49 | 0,5043 | 0,84 | 0,2113 |
| 0,15 | 0,4105 | 0,5 | 0,5000 | 0,85 | 0,1993 |
| 0,16 | 0,4230 | 0,51 | 0,4954 | 0,86 | 0,1871 |
| 0,17 | 0,4346 | 0,52 | 0,4906 | 0,87 | 0,1748 |
| 0,18 | 0,4453 | 0,53 | 0,4854 | 0,88 | 0,1623 |
| 0,19 | 0,4552 | 0,54 | 0,4800 | 0,89 | 0,1496 |
| 0,2 | 0,4644 | 0,55 | 0,4744 | 0,9 | 0,1368 |
| 0,21 | 0,4728 | 0,56 | 0,4684 | 0,91 | 0,1238 |
| 0,22 | 0,4806 | 0,57 | 0,4623 | 0,92 | 0,1107 |
| 0,23 | 0,4877 | 0,58 | 0,4558 | 0,93 | 0,0974 |
| 0,24 | 0,4941 | 0,59 | 0,4491 | 0,94 | 0,0839 |
| 0,25 | 0,5000 | 0,6 | 0,4422 | 0,95 | 0,0703 |
| 0,26 | 0,5053 | 0,61 | 0,4350 | 0,96 | 0,0565 |
| 0,27 | 0,5100 | 0,62 | 0,4276 | 0,97 | 0,0426 |
| 0,28 | 0,5142 | 0,63 | 0,4199 | 0,98 | 0,0286 |
| 0,29 | 0,5179 | 0,64 | 0,4121 | 0,99 | 0,0144 |
| 0,3 | 0,5211 | 0,65 | 0,4040 | ||
| 0,31 | 0,5238 | 0,66 | 0,3956 | ||
| 0,32 | 0,5260 | 0,67 | 0,3871 | ||
| 0,33 | 0,5278 | 0,68 | 0,3783 | ||
| 0,34 | 0,5292 | 0,69 | 0,3694 | ||
| 0,35 | 0,5301 | 0,7 | 0,3602 |
| n | Log2n | n | Log2n | n | Log2n |
| 0,0000 | 2,3219 | 3,1699 | |||
| 1,0000 | 2,5850 | 3,3219 | |||
| 1,5850 | 2,8074 | 5,6439 | |||
| 2,0000 | 3,0000 | 10 0 | 6,6439 |
Задача 1. Известно, что каждое из к возможных равновероятных двоичных сообщений несет 4 бита информации. Чему равно к?
Решение: H = log2k = 4 бита, следовательно, k=24=16. Таким образом, возможно 16 равновероятных двоичных сообщений, каждое из которых содержит 4 бита информации.
Задача 2. Дан алфавит [А1 А2, А3, А4] из которого составляют все возможные сообщения s длиной по три символа. Какое количество информации приходится на одно такое сообщение?
Решение: Найдем количество возможных сообщений s:
N=mn=43=64. Вычислим количество информации, содержащееся в одном сообщении s, составленном из исходного алфавита: I = log2 N= log2 64 = 6 бит
Задача 3. Дан алфавит мощностью 4, вероятности появления букв равны соответственно р1=р2=0,25; р3=0,34; р4 =0,16. Определить количество информации на символ сообщения, составленного из такого алфавита.
Решение: количество информации на символ алфавита есть энтропия данного алфавита. Так как символы алфавита неравновероятны, то энтропия равна
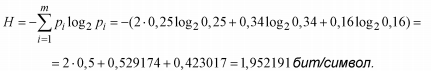
Задача 4. Чему равно количество информации при получении 16 сообщений равномерного четырехзначного троичного кода?
Решение. Мощность кодового алфавита т=3. В коде они комбинируются по 4, т. е. n=4. Число сообщений такого кода N=mn=34. Энтропия на одно сообщение Н = Iog2 N =4 Iog2 3. Количество информации в 16 сообщениях I=16 ∙4∙ log23= 101,44 бита.
Задача 5.Определить энтропию экрана мобильного телефона, если его разрешение 320x240, а каждый пиксель может отображать один из 4096 цветов.
Решение: предположим, что цвета пикселей равновероятны и взаимонезависимы, тогда энтропия одного пикселя Нп= Iog24096=12 бит. Всего пикселей 320*240=76800, а энтропия всего экрана Нэ=76800*12=921 600 бит.
Задача 6. Опытный индивидуальный предприниматель знает, что 25% всех его документов составляют налоговые декларации. Для неопытного предпринимателя появление любого типа документа - равновероятно. Определите, какое количество информации получит опытный и неопытный предприниматели при получении налоговой декларации?
Решение: для неопытного предпринимателя появление налоговой декларации или любого документа - равновероятно, следовательно
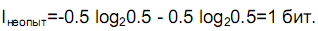
Опытный предприниматель заранее может предвидеть вероятность появления налоговой декларации, поэтому
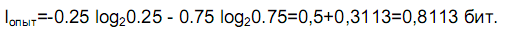
Задача 7. Чему равна энтропия системы, состоящей из к взаимное зависимых подсистем, если:
1) каждая подсистема состоит из п элементов, каждый из которых с равной вероятностью может находиться в т состояниях;
2) подсистема S1 состоит из п1 элементов, подсистема S2 состоит из п2 элементов и т.д., подсистема Sk состоит из пк элементов, каждый из которых может с равной вероятностью находиться в т состояниях;
3) каждая подсистема состоит из разного количества элементов, которые с разной вероятностью могут находиться в одном из состояний? Под энтропией системы понимается неопределенность того, что система будет находиться в одном из n возможных состояний.
Решение: 1) Находим энтропию одной подсистемы
H = log2 mn.
Общая энтропия системы равна сумме энтропии отдельных подсистем
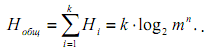
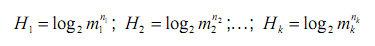 2) Определяем энтропию отдельных подсистем
2) Определяем энтропию отдельных подсистем
Общая энтропия системы
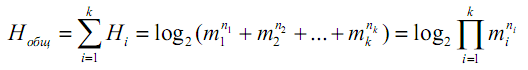
3) Определяем энтропию на один элемент подсистемы
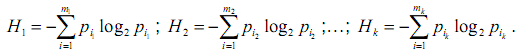
Определяем энтропию отдельных подсистем
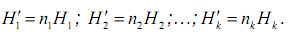
 Общая энтропия системы
Общая энтропия системы
Задача 8. Определить объем и количество информации в тексте «Широка страна моя родная», если для его передачи каждый символ заменяют 8 битами.
Решение: Число принятых символов, включая пробел, k = 24. Следовательно, объем передаваемой информации 24*8=192 бита. Количество информации: а) для равновероятного алфавита
Hi = log2 m = log2 32 = 5 бит/символ.
I, = kH1 = 24 • 5 = 120 бит;
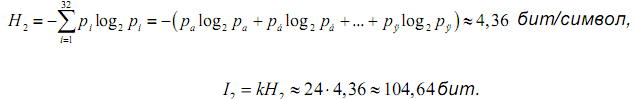 б) для неравновероятного алфавита (в этом и подобных случаях энтропия первичного алфавита не высчитывается каждый раз, а берется энтропия русского алфавита)
б) для неравновероятного алфавита (в этом и подобных случаях энтропия первичного алфавита не высчитывается каждый раз, а берется энтропия русского алфавита)
Задача 9. Известно, что количество натуральных блондинов и рыжих год от года уменьшается. Так в 1980 году вероятность встретить рыжего человека на улице составляла 16%, натурального блондина 16%, русоволосого 36%, а брюнета 32%. А в 2010 году рыжие встречаются с вероятностью 4%, натуральные блондины с вероятностью 8%, русоволосые - 64%, а брюнеты - 24%. В каком году было тяжелее верно угадать цвет волос случайного человека на улице?
 Решение: из теории известно, что чем больше энтропия некоторой группы событий, то тем тяжелее верно угадывать наступление следующего события. Вычислим энтропию для двух указанных случаев.
Решение: из теории известно, что чем больше энтропия некоторой группы событий, то тем тяжелее верно угадывать наступление следующего события. Вычислим энтропию для двух указанных случаев.
Так как H1980>H2010, то угадать вероятность цвета волос случайного человека на улице было сложнее в 1980 году.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Вычислите, какое количество информации приходится на одно сообщение длиной 3, 4, 5 и 6 символов, составленное из а) двоичного, б) троичного алфавита?
2. а) Чему равна максимальная энтропия системы, состоящей из двух элементов, каждый из которых может быть в двух состояниях? б) Чему равна энтропия системы, состоящей из трех элементов, каждый из которых может быть в четырех состояниях?; в) Чему равна энтропия системы, состоящей из четырех эле ментов, каждый из которых может быть в трех состояниях?
3. Дан алфавит мощностью 5. Определить количество информации на символ сообщения, составленного из этого алфавита:
а) если символы алфавита встречаются с равными вероятностями;
б) если символы алфавита встречаются в сообщении с вероятностями p1= 0,8; p2 = 0,15; р3= 0,03; р4 = 0,015; р5 = 0,005.
4. Чему равна неопределенность предпочтения одного из четырех государственных языков жителем Сингапура, если китайский предпочитают 30% жителей, малайский - 20%, английский - 40%, тамильский - 10%.
5. Определить объем передаваемых данных и количество информации в тексте «Получила тройку с плюсом, но вздремнула я со вкусом», если для его передачи каждый символ заменяют 7 битами.
6. Вероятность появления некоторого события в данном опыте равна р, вероятность того, что это событие не произойдет q = 1 - p. При каком значении q результат опыта будет обладать максимальной неопределенностью?
7. Для прибора Z детали из кладовой отдела комплектации доставляет конвейерная лента 1, для прибора Y — лента 2. В комплектующие изделия прибора Z входят 10 конденсаторов, 5 резисторов и 5 транзисторов; в комплектующие изделия прибора Y входят 8 конденсаторов, 8 резисторов и 4 транзистора. Вычислить в дитах энтропию появления одной из деталей каждого из приборов на ленте.
8. Чему равно количество информации при получении сообщения о
выходе из строя одного из восьми выключателей, произведенных в одно и тоже время на одном и том же заводе?
9. Специалисты знают, что каждый пятый фейерверк, запускаемый в нашей стране, выпускается фирмой «Праздник-праздник». Для неспециалистов запуск фейерверка любого производителя равновероятен. Определите, какое количество информации получит специалист и неспециалист при запуске фейерверка фирмы «Праздник-праздник»?
10. Сообщения составлены из равновероятного алфавита, содержащего 128 элементов. Чему равно количество символов в принятом сообщении, если известно, что оно содержит 42 бита информации? Чему равна энтропия этого сообщения?
11. Определить максимум энтропии системы, состоящей из 6 элементов, каждый из которых может быть в одном из четырех состояний равновероятно.
12. Экспериментальная модель робота-пылесоса может находиться в одном из 4 состояний: 1) с частотой 0,25 он пылесосит отлично; 2) в четвери случаев отказывается работать по непонятной причине; 3) в 30% случаев отказывается работать в связи с наступлением праздничных дней; 4) в двух случаях из 10 не работает в связи с необходимостью обновления его программного обеспечения. Определите энтропию робота и энтропию возможности проведения уборки этим роботом-пылесосом.
13. 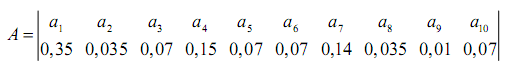 Определить энтропию источника сообщений, если статистика распределения вероятностей появления символов на выходе источника сообщений представлена следующей схемой:
Определить энтропию источника сообщений, если статистика распределения вероятностей появления символов на выходе источника сообщений представлена следующей схемой:
14. Дан алфавит, состоящий из 5 символов, вероятности появления которых равны соответственно: р1 = 0,7; р2 = 0,2; р3 = 0,08; р4= 0,015; р5 = 0,005. Определить количество информации сообщении, состоящем из 20 символов. Каким будет количество информации в данном сообщении, если все символы будут равновероятны?
15. Определить энтропию системы, состоящей из двух подсистем. Первая подсистема состоит из трех элементов, каждый из которых может находиться в двух состояниях с вероятностями р1=0,6; p2=0,4. Вторая подсистема состоит из двух элементов, каждый из которых может находиться в трех состояниях с вероятностями P1=0,1; р2=0,4; Р3=0,5.
16. Определить энтропию телевизионного изображения, воспроизводимого телевизионным приемником «Славутич-204», если у него разрешающая способность линий не менее 500, число градаций яркости 8, а условное число элементов строки — 700.
КОНТРОЛЬНЫЕ ЗАДАЧИ
1.Чему равно количество информации о неисправности n клавиш стандартной 101-клавишной клавиатуры?
2.В бою с трехголовым Змеем Горынычем Добрый Молодец отрубает ему одну голову в 20% случаев, 2 головы - с вероятностью 60%, 3 головы - в 20 % случаев. Во время боя Добрый Молодец может получить удар лапой с вероятностью 8%, ожог - с вероятностью 64%, упасть замертво в 28% боев. Чьи увечья после боя боле е неопределенны?
3.Определить объем и количество информации в принятом тексте: «Ищут пожарные, ищет милиция, ищут давно, но не могут найти.», если каждый символ кодируется 7 битами.
4.Разведчик MI-6 20% своего времени тратит на слежку за сотрудниками других разведок, 40% времени - на вербовку новых резидентов, а оставшееся время - на организацию дезинформации. Начальник отдела кадров 30% своего времени тратит на оформление документов, 40% - на учет рабочего времени сотрудников, а оставшееся время - на набор новых сотрудников. Сколько информации будет получено, если станет известно, что разведчик занят вербовкой? Чей вид деятельности разведчика или кадровика более неопределен?
5.Известно, что ученик школы на вопрос родителей о выполнении домашнего задания с одинаковой вероятностью отвечает, что задание выполнено или не выполнено. При этом, если ученик говорит о том, что задание не выполнено, то это всегда правда, а если ученик говорит, что задание выполнено, то это правда лишь в 6 случаях из 10. Вычислите количество информации следующих событий: а) ученик сказал, что выполнил задание и действительно его выполнил; б) ученик сказал, что выполнил задание, а в действительности его не выполнил; в) ученик сказал, что не выполнил задание и действительно его не выполнил; г) ученик сказал, что не выполнил задание, а на самом деле выполнил его; д) ученик на вопрос о домашнем задании сказал правду.
ОТВЕТЫ НА ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Для двоичного алфавита: 3, 4, 5, 6 бит; для троичного I=log233=4.75 бит, 6.34, 7.92, 9.51. 2. а) 2 бита, б) 6 бит, в) 6.32 бита. 3. а) Hmax=log25=2.32 бит/символ, б) Н=0.95 бит/символ. 4. Н=1.84 бит/символ. Н максимально при p=q. 7. Н1=0.4515 дит/символ; Н2=0.4581 дит/символ. 8. I=3 бита. 9. 1 бит, 0.468 бит. 10. 6 символов, Н=7 бит/символ. 11. 12 бит/состояние. 12. 1.98 бит; 0,81 бит. 13. 2,303 бит/символ. 14. 24.9 бит; 46,4 бита. 15. 5.63 бита. 16. 1050000 бит/изображение.
ЛИТЕРАТУРА
1. Вернер М. Основы кодирования. - М.: Техносфера, 2004.-288 с.
2. Цымбал В.П. Задачник по теории информации и кодированию. - Киев: Высшая Школа, 1976. - 276 с.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|