РАСЧЁТ МАКСИМАЛЬНОЙ ШИРИНЫ ПОЛОСЫ, ОЧИЩАЕМОЙ ОТ СНЕГА»

Лабораторная работа №1

«РАСЧЁТ МАКСИМАЛЬНОЙ ШИРИНЫ ПОЛОСЫ, ОЧИЩАЕМОЙ ОТ СНЕГА»

Цель работы: вывести регрессионную зависимость, позволяющую рассчитать допустимую ширину полосы обработки при очистке ВПП от снега для любого сочетания климатических условий.

Формулировка задачи

При определении максимальной ширины полосы, очищаемой от снега, с помощью номограммы (рис.) возможны ситуации, при которых нужны результаты, лежащие вне кривых, нанесённых на номограмму.

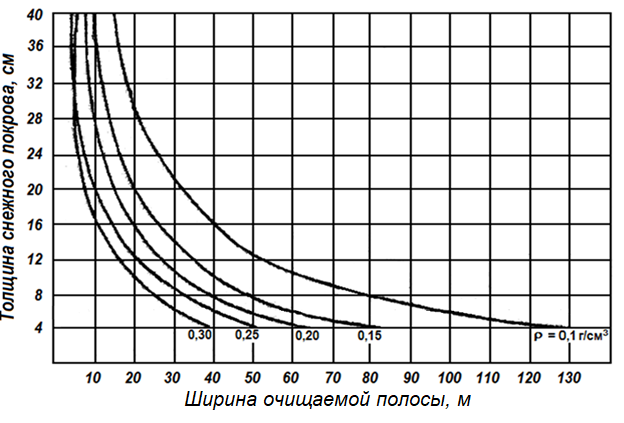
Рис. Номограмма определения ширины полосы, снег с которой образует снежный вал максимально допустимого поперечного сечения

Возможны два пути решения задачи:

· интерполяция внутри или за пределами диапазона имеющихся значений,

· описание кривых номограммы и трендов изменения их коэффициентов уравнениями регрессии.

Последний способ предпочтителен, так как предоставляет более широкие возможности учёта разнообразных условий эксплуатации.

При этом потребуется выполнить следующие действия:

1. Найти регрессионные зависимости допустимой ширины полосы обработки от толщины снежного покрова различной плотности.

2. Найти регрессионные зависимости коэффициентов и показателей степени в уравнениях регрессии от плотности снега.

3. Объединить полученные соотношения в единое выражение, позволяющее рассчитать допустимую ширину полосы обработки для снежного покрова любой толщины и любых плотности.

Порядок выполнения работы

1. Сохраняем номограмму в формате рисунка, который копируем в свою именную папку.

2. В этой же папке создаём именной файл «Отчёт.xls» в редакторе Excel.

3. Открываем рисунок в редакторе Paint, (стандартная программа Microsoft Office), сохраняем его в своей папке и определяем цену одного деления по каждой из осей номограммы: по оси абсцисс в м/пиксель, по оси ординат в см/пиксель.

4. Определяем координаты точек пересечения всех кривых номограммы со всеми линиями сетки координат: по осям абсцисс (в м) и ординат(в мм).

5. На листе 1 файла «Отчёт.xls» строим таблицу (табл. 1), в которую заносим координаты всех точек пересечения кривых номограммы с линиями сетки координат в натуральных единицах измерения.

Таблица 1.

Толщина снежного покрова, см	Ширина полосы очистки, м
Толщина снежного покрова, см	0,10 г/см³	0,15 г/см³	0,20 г/см³	0,25 г/см³	0,30 г/см³


…	…	…	…	…	…

6. На этом же листе файла «Отчёт1.xls» строим диаграмму «толщина снежного покрова – ширина полосы очистки» для плотности снега 0,10 г/см³ и выбираем аппроксимирующую кривую. Полученное регрессионное уравнение записываем в ячейку под соответствующим столбцом.

7. Критерием верности подбора аппроксимирующей кривой и описывающего её уравнения во всех случаях является величина среднеквадратичного отклонения экспериментальных точек от выбранной кривой.

8. Диаграмму удаляем и повторяем процедуру, описанную в п. 6, для оставшихся значений плотности снежного покрова.

9. На листе 2 файла «Отчёт.xls» строим таблицу (табл. 2) со значениями коэффициентов и показателей степени уравнений, полученных в п.п. 7 и 8.

Таблица 2.

Толщина снежного покрова, см	Коэффициенты при аргументе	Показатели степени, в которую возводится аргумент


…

10. На этом же листе файла «Отчёт1.xls» создаём диаграмму «толщина снежного покрова – коэффициент при аргументе» и выбираем аппроксимирующую кривую №1. Описывающее её регрессионное уравнение №1 записываем в ячейку под соответствующим столбцом.

11. На этом же листе удаляем предыдущую диаграмму, и строим диаграмму «толщина снежного покрова – показатель степени при аргументе» и выбираем аппроксимирующую кривую №2. Описывающее её регрессионное уравнение №2 записываем в ячейку под соответствующим столбцом.

В результате получаем зависимость

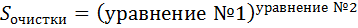
где S_{очистки} - ширина полосы очистки, м.

Отчёт

Отчётом о выполненной лабораторной работе является электронный файл «Отчёт.xls», защищаемый студентом, и его бумажная копия, подписанная преподавателем и остающаяся у студента.