Ключи, критерии оценивания заданий школьного этапа

Ключи, критерии оценивания заданий школьного этапа

Всероссийской олимпиады школьников

2020-2021 учебный год

Математика

9 класс

Максимальный балл – 25

Задание 1. (7 баллов) 45 конфет стоят столько же рублей, сколько их можно купить на 20 рублей. Сколько конфет можно купить на 50 рублей?

Ответ: 75 конфет.

Решение. Пусть х – стоимость одной конфеты в рублях.

Тогда 45х = 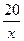, откуда х = .

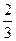И тогда на 50 рублей можно купить 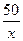= 75 конфет.

Критерии

	Любое верное решение
	Верно составлено уравнение 45х = 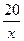, но при его решении или в дальнейшем допущена арифметическая ошибка
	В решении утверждается, что цена одной конфеты равна 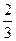, проверяется, что такая стоимость подходит в условие задачи, и получен верный ответ
	Приведён только верный ответ
	Неверный ответ

Задание 2. (4 балла) Назовём трёхзначное число интересным, если хотя бы одна его цифра делится на 3. Какое наибольшее количество подряд идущих интересных чисел может быть?

Ответ: 122.

Решение. Числа 289, 290, . . . , 299, 300, . . . , 399, 400, . . . , 409, 410 являются интересными (напомним, что 0 делится на 3), и их всего 122. Докажем, что большего количества быть не может.

Предположим, что нам удалось найти большее количество подряд идущих интересных чисел; выберем из них 123 подряд идущих.

Назовём сотню подряд идущих чисел, у которых разряд сотен одинаков и делится на 3, интересной сотней. Заметим, что до любой интересной сотни идут только 11 интересных чисел, оканчивающихся на 89, 90, . . . , 99, а 12-е число оканчивается на 88 и интересным не будет. Аналогично после интересной сотни идут тоже только 11 интересных чисел, оканчивающихся на 00, . . . , 09, 10, а 12-е число оканчивается на 11 и также не интересное.

Если наша последовательность из 123 чисел пересекается с некоторой интересной сотней, то она содержит хотя бы 12 чисел либо до, либо после этой сотни.

Следовательно, хотя бы одно число в ней не интересное.

Если же наша последовательность из 123 чисел не пересекается с интересной сотней, то она содержит хотя бы одно число, оканчивающееся на 55 (как и на любую другую комбинацию цифр). Но это число не интересное, так как ни один разряд в нём на 3 не делится.

Критерии

Приведён верный ответ, верный пример и обоснование

Приведён верный пример и ответ, но нет обоснования, что большее количество чисел невозможно

Приведён верный пример, но в нем неправильно посчитано количество чисел

Приведён верный ответ

Неверный ответ и неверный (или отсутствующий) пример

Задание 3(7 баллов).На рисунке изображён график приведённого квадратного трёхчлена (ось ординат стёрта, расстояние между соседними отмеченными точками равно 1). Чему равен дискриминант этого трёхчлена?

Решение. Пусть х₁и х₂- корни данного трёхчлена (х₁<х₂). Из условия следует, что х₂– х₁ = 2 . Поскольку 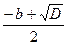х₂ = _,х_{1= ,}получаем, что х₂– х₁ = , откуда D = 4.

Ответ: 4.

Критерии

Приведён верный ответ, обоснование

Найдена разность корней приведённого квадрат уравнения

Написана формула корней приведённого квадратного уравнения

Приведён верный ответ

Неверный ответ или ответ отсутствует

Задание 4(7 баллов). Вокруг цилиндрической колонны высотой 20 метров и диаметром 3 метра обвита лента, которая поднимается от подножия до вершины семью полными витками. Какова длина ленты?

Решение. Разрезав цилиндр вдоль образующей его боковой поверхности, проходящей через начало ленты, и развернув эту поверхность, получим прямоугольник ABCD размером 20 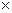3π (см. рисунок).

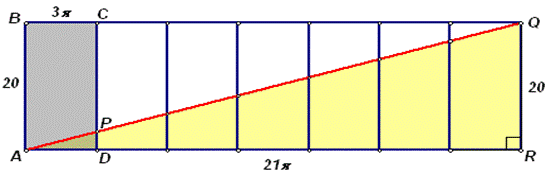
«Приклеив» к нему ещё шесть таких же прямоугольников, получим прямоугольник ABQR. На этой развёртке первый виток ленты предстанет в виде отрезка AP, а вся лента развернётся в диагональ AQ прямоугольника ABQR.

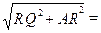
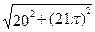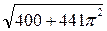
Значит, её длина l = AQ = = 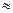68,9(метров).

Критерии

	Верное обоснованное решение задачи.
	Приведены верные рассуждения, являющиеся решением задачи , но сделана вычислительная ошибка
	Приведены в целом верные рассуждения, в которых допущены ошибки, не имеющие для решения принципиального характера и дан верный ответ.
	Приведено верное решение задачи при отсутствии обоснований: указаны все промежуточные выводы без указаний связей между ними (ссылки на теоремы или определения).
	Сделаны дополнительные построения и обозначения на чертеже, из которых ясен ход решения, но не приведены сами рассуждения, дан верный ответ.
	Найдена верно длина окружности для 1 витка ленты.
	Приведён верный ответ.
	Неверный ответ и неверный (или отсутствующий) пример.

12 Следующая ⇒