
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дисциплина: «Математика». Преподаватель: Григорьева Н.С.. Лекция № 2. Тема. Производная функции. Дифференциал и его приложение к приближенным вычислениям.
Дисциплина: «Математика»
Преподаватель: Григорьева Н.С.
Лекция № 2
Тема. Производная функции. Дифференциал и его приложение к приближенным вычислениям.
Перейдем к основным идеям одного из важнее разделов математики – дифференциального исчисления. Методы дифференциального исчисления дают возможность свести изучение сложного процесса к более простому – равномерному, найти его скорость и ускорение, определить условия оптимального прохождения процесса, оценить допущенные погрешности, построить графики и др. Дифференциальное исчисление – раздел математики, в котором рассматривается исследования функций с помощью производных и дифференциалов.
1. Задачи, которые приводят к понятию производной
Задача 1 (о мгновенной скорости). Пусть некоторая материальная точка движется по оси x, так что x(t) есть координата точки в момент времени t. Спустя время координата точки будет , т.е. за время точка пройдет путь . Поэтому средняя скорость точки за интервал времени будет равна . Чтобы найти мгновенную скорость точки в момент времени надо устремить к нулю.
Задача 2 (о скорости химической реакции) (t) есть количество вещества прореагировавшего за время t. Спустя время количество прореагировавшего вещества будет , т.е. за время количество прореагировавшего вещества . Поэтому средняя скорость химической реакции за интервал времени будет равна . Чтобы найти мгновенную скорость химической реакции в момент времени надо устремить к нулю, то естьgПусть
Поскольку с помощью предела решают кроме рассмотренных ещё и много других важнейших задач (например: задача о величине переменного тока, который течет в проводнике; нахождении линейной плотности неоднородного стержня, теплоемкости тела при его нагревании, угловой скорости тела, которое вращается и многие др), то целесообразно всесторонне изучить данный предел, в частности, указать способы его вычисления. Этот предел в математике и носит название производной.
2. Производная, ее геометрический и физический смысл
Определение: Производной данной функции y=f(x) называется предел отношения приращения функции Δy к приращению аргумента Δx, когда последнее стремится к нулю и такой предел существует и конечен.
Заметим, что производную можно рассматривать как функцию аргумента x. Эта функция обозначается f '(x)
Производная обозначается символами f'(x), y',  . Конкретное значение производной при x=a обозначается f'(a) или y'|x=a.
. Конкретное значение производной при x=a обозначается f'(a) или y'|x=a.
Операция нахождения производной от функции f(x) называется дифференцированием этой функции.
Для непосредственного нахождения производной по определению можно применить следующее практическое правило:
1. Придать x приращение Δx и найти наращенное значение функции f(x + Δx).
2. Найти приращение функции Δy = f(x + Δx) – f(x).
3. Составить отношение и найти предел этого отношения при Δx→0.
Примеры.
1. Найти производную функции y = x2
а) в произвольной точке;
б) в точке x= 2.
а)
1.
1. f(x + Δx) = (x + Δx)2;
2. Δy = (x + Δx)2 – x2=2xΔx– x2;
3.  .
.
б) f '(2) = 4
2. Используя определение найти производную функции 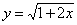 в произвольной точке.
в произвольной точке.
1.  .
.
2. 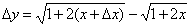
3. 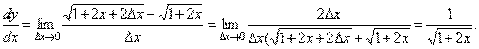
Учитывая задачи о мгновенной скорости и касательной к графику легко построить следующие утверждения:
Физический смысл производной: скорость неравномерного движения это производная от пройденного пути по времени.
Геометрический смысл производной: у'(x0) представляет угловой коэффициент касательной к графику этой функции в точке x0 (т.е. при данном значении аргумента x, производная равна тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке М0(x;y) с положительным направлением оси Ox).
Определение. Касательной к графику функции в точке М0(x0, y0) назовем предельное положение секущей М0М, когда точка М, двигаясь вдоль кривой, стремиться к совпадению с точкой М0..
Уравнение касательной к графику функции в точке М0 (x0, y0):
.
(вывод формулы самостоятельно, у=kx+b-уравнение прямой, k= )
3. Производная суммы/разности
Итак, мы дали определение производной, объяснили ее физический и геометрический смысл. Теперь необходимо сделать следующий шаг - рассмотреть правила дифференцирования.
Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x.
Основные правила дифференцирования выражаются формулами:
Производная от любого числа равна нулю:
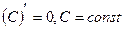
Производная произведения постоянной на функции:
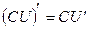
Производная алгебраической суммы функций:
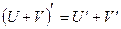
Производная произведения функций:

Производная частного (дроби):

Производная сложной функции:
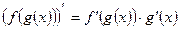
Доказательство формулы 1.
Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx).
Тогда
Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv.
Следовательно,
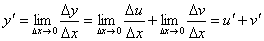 .
.
(построить вывод следствия)
4. Производная произведения/частного
Доказательство формулы 2.
Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому
Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x).
Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δx)→u(x), v(x+Δx)→v(x), при Δx→0.
Поэтому можем записать
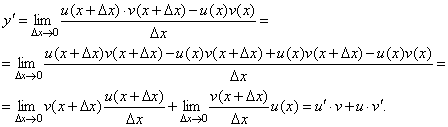
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.
Пусть, например, y=u·v·w. Тогда,
y ' = u '·(v·w) + u·(v ·w) ' = u '·v·w + u·(v '·w +v·w ') = u '·v·w + u·v '·w + u·v·w '.
(построить вывод следствия)
Доказательство формулы 3.
Пусть 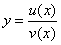 . Тогда
. Тогда
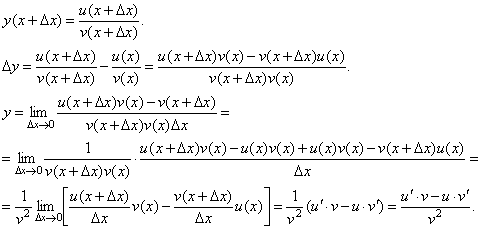
При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0.
(построить вывод следствий)
Производные функций
Элементарные функции
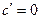 (с - постоянная)
х¢ = 1 (с - постоянная)
х¢ = 1
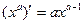 (а - постоянная) (а - постоянная)
| Частные случаи
а) 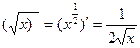 ;
б) ;
б) 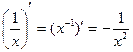 ; ;
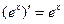

 ; ; 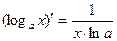
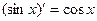 ; ; 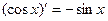
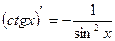 ; ; 
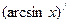 ¢ = ¢ = 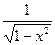
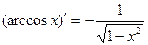
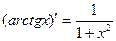
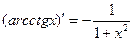
|
Сложные функции
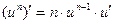
| Частные случаи
а)  б)
б) 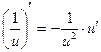
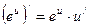  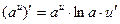
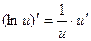 ; ; 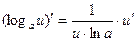
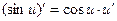
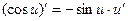
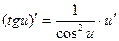
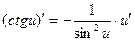
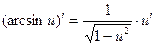

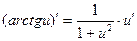
 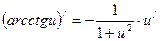
|
Дифференциалом функции у=ƒ(х) (или дифференциалом первого порядка) называется произведение производной этой функции ƒ΄(х) на
произвольное приращение аргумента Δх:
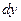 = ƒ΄(х) Δх
= ƒ΄(х) Δх
Дифференциал аргумента равен приращению аргумента: dх=Δх. Поэтому дифференциал функции равен произведению ее производной на дифференциал аргумента:
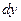 = ƒ΄(x)
= ƒ΄(x) 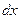 , ƒ΄(x) =
, ƒ΄(x) = 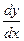
Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка:
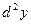 = ƒ΄΄(x)
= ƒ΄΄(x)  ,
,
т.е. дифференциал второго порядка функции у=ƒ(х) равен произведению второй производной этой функции на квадрат дифференциала аргумента.
Пример 1
Вычислить приближенно 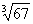 , заменяя приращения функции ее дифференциалом.
, заменяя приращения функции ее дифференциалом.
Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала:
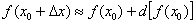
Начинаем разбираться, здесь всё просто!
На первом этапе необходимо составить функцию 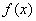 . По условию предложено вычислить кубический корень из числа:
. По условию предложено вычислить кубический корень из числа: 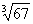 , поэтому соответствующая функция имеет вид:
, поэтому соответствующая функция имеет вид: 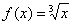 . Нам нужно с помощью формулы найти приближенное значение
. Нам нужно с помощью формулы найти приближенное значение 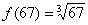 .
.
Смотрим на левую часть формулы 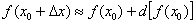 , и в голову приходит мысль, что число 67 необходимо представить в виде
, и в голову приходит мысль, что число 67 необходимо представить в виде  . Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе:
. Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе:
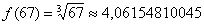 – получилось 4 с хвостиком, это важный ориентир для решения.
– получилось 4 с хвостиком, это важный ориентир для решения.
В качестве 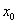 подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение
подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение 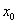 должно быть как можно ближе к 67. В данном случае:
должно быть как можно ближе к 67. В данном случае:  . Действительно:
. Действительно: 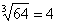 .
.
Примечание: Когда с подбором 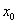 всё равно возникает затруднение, просто посмотрите на скалькулированное значение (в данном случае
всё равно возникает затруднение, просто посмотрите на скалькулированное значение (в данном случае 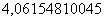 ), возьмите ближайшую целую часть (в данном случае 4) и возведите её нужную в степень (в данном случае
), возьмите ближайшую целую часть (в данном случае 4) и возведите её нужную в степень (в данном случае 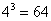 ). В результате и будет выполнен нужный подбор:
). В результате и будет выполнен нужный подбор:  .
.
Если  , то приращение аргумента:
, то приращение аргумента: 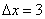 .
.
Итак, число 67 представлено в виде суммы 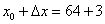
Далее работаем с правой частью формулы 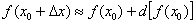 .
.
Сначала вычислим значение функции в точке  . Собственно, это уже сделано ранее:
. Собственно, это уже сделано ранее:
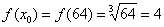
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|