ОТНОШЕНИЯ НА МНОЖЕСТВЕ. Свойства отношений

ОТНОШЕНИЯ НА МНОЖЕСТВЕ

Связи между элементами двух множеств называют соответствиями, а связи между элементами одного множества называют отношениями.

Если рассматривают отношения между двумя элементами множества, то их называют бинарными, между тремя элементами – тернарными, между n элементами – n-арными.

§1. Понятие бинарного отношения на множестве

Прежде,чем определить понятие бинарного отношения, рассмотрим конкретный пример.

Пример. На множестве Х={2,4,6,8} задано отношение «меньше». 2 < 4; 2 < 6; 2 < 8; 4 < 6; 4 < 8; 6 < 8.Полученные неравенства можно записать (2; 4); (2; 6); (2; 8); (4; 6); (4; 8); (6; 8). Но все эти пары есть элементы декартова произведения Х×Х,

т.е. бинарное отношение является подмножеством Х×Х.

Опр. Бинарным отношением на множествеХ называют всякое подмножество декартова произведения Х×Х.

Так как в дальнейшем будем рассматривать только бинарные отношения, то слово «бинарные можно опускать»

Отношения будем обозначать R, S,T,P, … хRу; (х; у) 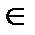R

Способы задания: перечисление пар, с помощью графа, на символическом языке.

n. На множестве Х={2,4,6,8}рассмотрим отношение R – «быть кратным»

2 4 символически:

«быть меньше» «х < у»

«быть кратным» «х 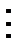у»

«х больше у на 3» можно записать в виде равенства х – у = 3 (х = у + 3)

8 6

Для R, заданного на множестве Х всегда можно найти обратное отношение R^-1.

Если хRу , то уR^-1х .

§2. Свойства отношений

Опр. Отношение R на множестве Х называют рефлексивным, если о каждом элементе можно сказать, что он находится в отношении R сам с собой.

х R х R рефлексивно на.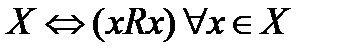

Привести пример рефлексивных отношений. Например: на множестве студентов ИПиП «обучаться в одной группе», на множестве комсомольчан R- «проживать в одном доме», на множестве всех треугольников задано отношение «быть подобными».

Опр. Отношение R на множестве Х называют антирефлексивным, если о каждом элементе можно сказать, что он не находится в этом отношении сам с собой.

Rантирефлексивно на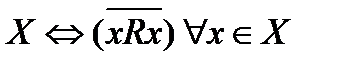

Опр. Отношение R на множестве Х называют симметричным, если выполняется условие: из того, что элемент х находится в отношении R с элементом у, следует, что и элемент у находится в отношенииR с элементом х.

R симметрично на .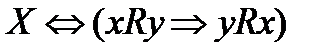

Примером симметричных отношений являются: на множестве студентов ИПиП «обучаться в одной группе», на множестве комсомольчан R- «проживать в одном доме», на множестве всех треугольников задано отношение «быть подобными».

Опр. Отношение R на множестве Х называют антисимметричным, если для различных элементов х и у из множества Х выполняется условие: из того, что х находится в отношении R с у , следует, что элемент у не находится в этом отношении с элементом х .

Опр. Отношение R на множестве Х называют транзитивным, если выполняется условие: из того, что элемент хнаходится в отношении Rcэлементом у и элемент у находится в отношении Rс элементом z, следует, что элемент х находится в отношении R с элементом z, т.е.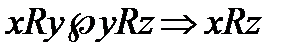

х••у

•

п. Построить граф отношения: 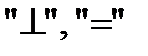длиннее

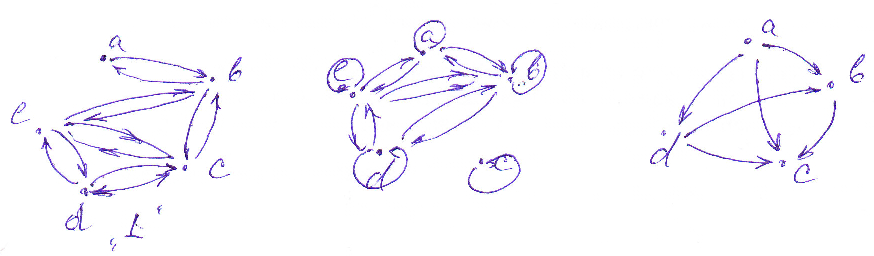
п.

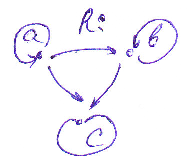Отношение задано графом. Доказать, что R рефлексивно, антисимметрично и транзитивно.

п. 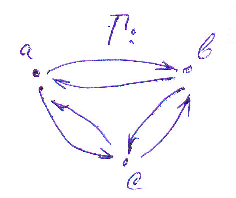какими свойствами обладает отношение Т?

12 Следующая ⇒