Лабораторная работа №1 по теме «Анализ распределения признака»

Лабораторная работа №1 по теме «Анализ распределения признака»

Цель: проанализировать распределение признака в статистической совокупности с использованием средств MS Excel и сделать выводы.

Задача: выполнить с помощью средств MS Excel статистическое исследование структуры и формы распределения признака в статистической совокупности.

Исходные данные:

выборка значений признака-фактора Х (порядок формирования см. в п.1 задания)

Задание:

1. Сгенерировать выборку значений нормально распределенного признака Х с заданными параметрами (Хср и СКО) согласно варианту (см. приложение к лабораторной работе №1).

Для этого использовать встроенное средство MS Excel пакет «Анализ данных»: Главное меню ®Данные® Анализ данных ®Генерация случайных чисел:

СКО

Хср

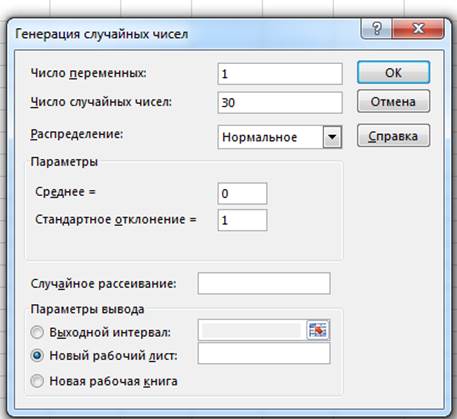
где значения Хср и СКО взять из таблицы с вариантами (Прил.1)

В результате должен сформироваться столбец числовых значений (30 значений) нормально распределенного признака Х.

2. Построить ряды распределения - структурные группировки:

▪ равноинтервальный ряд (таблицу, гистограмму, кумуляту) – ряд №1.

▪ равнонаполненный ряд (таблицу) –ряд №2.

(количество групп, определяется по формуле Стерджесса: k=1+3,322*lg N (N-объем совокупности);

3. Рассчитать показатели центра измерения признака:

среднее значение, медиана, мода по несгруппированным данным и по сгруппированным данным (ряд №1).

4. Рассчитать показатели структуры распределения признака:

1 и 3 квартили, 1-ую и 9-ую децили несгруппированным данным и по сгруппированным данным (ряд №1).

Построить диаграмму с усами по несгруппированным данным.

5. Рассчитать показатели вариации признака:

размах вариации, среднее линейное отклонение, дисперсия генеральная, среднее квадратическое отклонение генеральное, дисперсия исправленная (выборочная), среднее квадратическое отклонение исправленное (выборочное), коэффициент вариации по несгруппированным данным.

По сгруппированным данным (ряд№1) рассчитать показатели: генеральные дисперсию и СКО (среднее квадратическое отклонение).

6. Рассчитать показатели формы распределения признака:

коэффициент асимметрии, эксцесс по несгруппированным данным и по сгруппированным данным (ряд №1).

7. Проверить гипотезы о нормальности распределения признака с помощью критерия Пирсона («хи-квадрат»). Для этого использовать ряд №2.

12 Следующая ⇒